题目内容
10.已知函数f(x)=ex-2ax,函数g(x)=-x3-ax2.若不存在x1,x2∈R,使得f′(x1)=g′(x2),则实数a的取值范围为( )| A. | (-2,3) | B. | (-6,0) | C. | [-2,3] | D. | [-6,0] |
分析 先求导,分别求出导函数的最值,再根据不存在x1,x2∈R,使得f′(x1)=g′(x2),得到关于a的不等式解得即可.
解答 解:∵函数f(x)=ex-2ax,函数g(x)=-x3-ax2,
∴f′(x)=ex-2a>-2a,g′(x)=-3x2-2ax=-3(x+$\frac{a}{3}$)2+$\frac{{a}^{2}}{3}$≤$\frac{{a}^{2}}{3}$,
∵不存在x1,x2∈R,使得f′(x1)=g′(x2),
∴-2a≥$\frac{{a}^{2}}{3}$,
解得-6≤a≤0,
故选:D.
点评 本题考查了导数的运算法则和函数的最值问题,以及不等式的解法,属于中档题.

练习册系列答案
相关题目
13.已知{an}满足a1=1,a2=1,an+2-an+1-an=0,x1,x2是方程x2=x+1两根.求证:
(1)数列{an+1-x1an},和{an+1-x2an}均为等比数列.
(2)求an=?
(1)数列{an+1-x1an},和{an+1-x2an}均为等比数列.
(2)求an=?
5.在等差数列{an}中,a4=2,且a1+a2+…+a10=65,则公差d的值是( )
| A. | 4 | B. | 3 | C. | 1 | D. | 2 |
2.已知等差数列{an}的前n项和为Sn,公差为d,若$\frac{{S}_{2016}}{2016}$-$\frac{{S}_{16}}{16}$=100,则d的值为( )
| A. | $\frac{1}{20}$ | B. | $\frac{1}{10}$ | C. | 10 | D. | 20 |
20. 某市小型机动车驾照“科二”考试共有5项考察项目,分别记作①,②,③,④,⑤
某市小型机动车驾照“科二”考试共有5项考察项目,分别记作①,②,③,④,⑤
(Ⅰ)某教练将所带10名学员“科二”模拟考试成绩进行统计(如表所示),并打算从恰有2项成绩不合格的学员中任意抽出2人进行补测(只侧不合格项目),求补测项目种类不超过3项的概率.
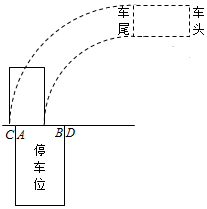
(Ⅱ)如图,某次模拟演练中,教练要求学员甲倒车并转向90°,在车边缘不压射线AC与射线BD的前提下,将汽车驶入指定的停车位.根据经验,学员甲转向90°后可使车尾边缘完全落在线段CD上,且位于CD内各处的机会相等.若CA=BD=0.3m,AB=2.4m,汽车宽度为1.8m,求学员甲能按教练要求完成任务的概率.
 某市小型机动车驾照“科二”考试共有5项考察项目,分别记作①,②,③,④,⑤
某市小型机动车驾照“科二”考试共有5项考察项目,分别记作①,②,③,④,⑤(Ⅰ)某教练将所带10名学员“科二”模拟考试成绩进行统计(如表所示),并打算从恰有2项成绩不合格的学员中任意抽出2人进行补测(只侧不合格项目),求补测项目种类不超过3项的概率.
| 项目/学号编号 | ① | ② | ③ | ④ | ⑤ |
| (1) | T | T | T | ||
| (2) | T | T | T | ||
| (3) | T | T | T | T | |
| (4) | T | T | T | ||
| (5) | T | T | T | T | |
| (6) | T | T | T | ||
| (7) | T | T | T | T | |
| (8) | T | T | T | T | T |
| (9) | T | T | T | ||
| (10) | T | T | T | T | T |
| 注:“T”表示合格,空白表示不合格 | |||||
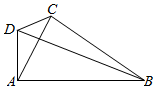 在如图所示的四边形ABCD中,∠BAD=90°,∠BCD=120°,∠BAC=60°,AC=2,记∠ABC=θ.
在如图所示的四边形ABCD中,∠BAD=90°,∠BCD=120°,∠BAC=60°,AC=2,记∠ABC=θ.