题目内容
5.抛物线x2=-14y的焦点坐标是(0,-$\frac{7}{2}$),准线方程是y=$\frac{7}{2}$.分析 直接利用抛物线方程求出焦点坐标与准线方程即可.
解答 解:抛物线x2=-14y的焦点坐标是:(0,-$\frac{7}{2}$),准线方程是:y=$\frac{7}{2}$.
故答案为:(0,-$\frac{7}{2}$);y=$\frac{7}{2}$.
点评 本题考查抛物线的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
13.已知不等式组$\left\{\begin{array}{l}3x+4y-10≥0\\ x≤4\\ y≤3\end{array}\right.$表示区域D,过区域D中任意一点P作圆x2+y2=1的两条切线且切点分别为A,B,当∠PAB最小时,cos∠PAB=( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{{\sqrt{3}}}{2}$ | D. | -$\frac{1}{2}$ |
20. 某市小型机动车驾照“科二”考试共有5项考察项目,分别记作①,②,③,④,⑤
某市小型机动车驾照“科二”考试共有5项考察项目,分别记作①,②,③,④,⑤
(Ⅰ)某教练将所带10名学员“科二”模拟考试成绩进行统计(如表所示),并打算从恰有2项成绩不合格的学员中任意抽出2人进行补测(只侧不合格项目),求补测项目种类不超过3项的概率.
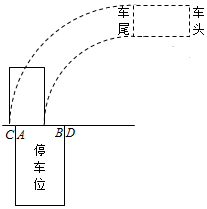
(Ⅱ)如图,某次模拟演练中,教练要求学员甲倒车并转向90°,在车边缘不压射线AC与射线BD的前提下,将汽车驶入指定的停车位.根据经验,学员甲转向90°后可使车尾边缘完全落在线段CD上,且位于CD内各处的机会相等.若CA=BD=0.3m,AB=2.4m,汽车宽度为1.8m,求学员甲能按教练要求完成任务的概率.
 某市小型机动车驾照“科二”考试共有5项考察项目,分别记作①,②,③,④,⑤
某市小型机动车驾照“科二”考试共有5项考察项目,分别记作①,②,③,④,⑤(Ⅰ)某教练将所带10名学员“科二”模拟考试成绩进行统计(如表所示),并打算从恰有2项成绩不合格的学员中任意抽出2人进行补测(只侧不合格项目),求补测项目种类不超过3项的概率.
| 项目/学号编号 | ① | ② | ③ | ④ | ⑤ |
| (1) | T | T | T | ||
| (2) | T | T | T | ||
| (3) | T | T | T | T | |
| (4) | T | T | T | ||
| (5) | T | T | T | T | |
| (6) | T | T | T | ||
| (7) | T | T | T | T | |
| (8) | T | T | T | T | T |
| (9) | T | T | T | ||
| (10) | T | T | T | T | T |
| 注:“T”表示合格,空白表示不合格 | |||||
17.设点(x,y)在平面区域E内,记事件A“对任意(x,y)∈E,有2x-y≥1”,则满足事件A发生的概率P(A)=1的平面区域E可以是( )
| A. | $\left\{\begin{array}{l}{x≤2}\\{x+y≥0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x≥2}\\{x+y≤0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x≥2}\\{x-y≤0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x≤2}\\{x-y≥0}\end{array}\right.$ |
14.在平面直角坐标系内,以原点O为顶点,x轴非负半轴为始边,任作一角,该角的终边OA落在第一象限的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
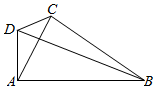 在如图所示的四边形ABCD中,∠BAD=90°,∠BCD=120°,∠BAC=60°,AC=2,记∠ABC=θ.
在如图所示的四边形ABCD中,∠BAD=90°,∠BCD=120°,∠BAC=60°,AC=2,记∠ABC=θ.