题目内容
2.若函数f(x)=lnx+ax2-(a+2)x在$x=\frac{1}{2}$处取得极大值,则正数a的取值范围是(0,2).分析 求出函数的导数,通过讨论a的范围,求出函数的单调区间,从而求出函数的极值点,结合已知条件,判断即可.
解答 解:f(x)的定义域是(0,+∞),
f′(x)=$\frac{1}{x}$+2ax-(a+2)=$\frac{(2x-1)(ax-1)}{x}$,
①a≤0时,ax-1<0,
令f′(x)>0,解得:x>$\frac{1}{2}$,令f′(x)<0,解得:0<x<$\frac{1}{2}$,
故$\frac{1}{2}$是函数的极小值点,不合题意,
②0<a<2时,$\frac{1}{2}$<$\frac{1}{a}$,
令f′(x)>0,解得:x<$\frac{1}{2}$或x>$\frac{1}{a}$,
令f′(x)<0,解得:$\frac{1}{2}$<x<$\frac{1}{a}$,
∴f(x)在(0,$\frac{1}{2}$)递增,在($\frac{1}{2}$,$\frac{1}{a}$)递减,在($\frac{1}{a}$,+∞)递增,
∴函数f(x)在$x=\frac{1}{2}$处取得极大值,符合题意,
③a=2时,f′(x)≥0,f(x)递增,无极值,
④a>2时,$\frac{1}{2}$>$\frac{1}{a}$,
令f′(x)>0,解得:x>$\frac{1}{2}$或x<$\frac{1}{a}$,
令f′(x)<0,解得:$\frac{1}{a}$<x<$\frac{1}{2}$,
∴f(x)在(0,$\frac{1}{a}$)递增,在($\frac{1}{a}$,$\frac{1}{2}$)递减,在($\frac{1}{2}$,+∞)递增,
∴函数f(x)在x=$\frac{1}{a}$处取得极大值,不符合题意,
综上,a∈(0,2),
故答案为:(0,2).
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及分类讨论思想,是一道中档题.

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案| A. | -24 | B. | -9 | C. | -12 | D. | 24 |
| A. | 2b-$\frac{4}{3}$ | B. | $\frac{3}{2}$b-$\frac{2}{3}$ | C. | 0 | D. | b2-$\frac{1}{6}$b3 |
| A. | 0和-4 | B. | 0;b取任意实数 | C. | 0和4 | D. | 4;b取任意实数 |
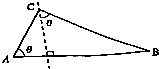 某人以速度vm/min的速度从点A沿东偏北θ方向走3min到达点C后,再沿南偏东θ方向走4min到达B点,AB=100m,求他走路的最小速度.
某人以速度vm/min的速度从点A沿东偏北θ方向走3min到达点C后,再沿南偏东θ方向走4min到达B点,AB=100m,求他走路的最小速度.