题目内容
11.设A={x|x2+ax+b=0},B={x|x2+cx+15=0}.若A∩B={3},A∪B={1,3,5},试求实数a,b,c的值.分析 根据A∩B={3},A∪B={1,3,5},B={x|x2+cx+15=0},先求出集合B,进而可求出集合A,由此可得实数a,b,c的值.
解答 解:∵A∩B={3},
∴3∈A且3∈B.
∴9+3c+15=0,即c=-8,
∴B={x|x2-8x+15=0}={3,5},又A∩B={3},A∪B={1,3,5},
∴A={1,3},
故1,3是方程x2+ax+b=0的两根,由根与系数的关系得$\left\{\begin{array}{l}{1+3=-a}\\{1×3=b}\end{array}\right.$
∴$\left\{\begin{array}{l}{a=-4}\\{b=3}\end{array}\right.$
点评 本题主要考查一元二次方程根与系数的关系,两个集合的交集、并集的定义和求法,属于中档题.

练习册系列答案
相关题目
7.已知各项为正的数列{an}的前n项的乘积为Tn,点(Tn,n2-15n)在函数y=log2x的图象上,则数列{log2an}的前10项和为( )
| A. | -140 | B. | -50 | C. | 124 | D. | 156 |
6.已知函数f(x)=ex(x2+2ax+b)在x=-1处取得极大值t,则t的取值范围是( )
| A. | ($\frac{2}{e}$,+∞) | B. | (-∞,$\frac{2}{e}$) | C. | (-$\frac{2}{e}$,+∞) | D. | (-∞,-$\frac{2}{e}$) |
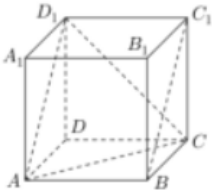 如图,正方体ABCD-A1B1C1D1,则下列四个命题:
如图,正方体ABCD-A1B1C1D1,则下列四个命题: