题目内容
10.下列函数中,既是奇函数又是增函数的为( )| A. | y=-x2 | B. | $y=\frac{-1}{x}$ | C. | $y=x+\frac{1}{x}$ | D. | y=x|x| |
分析 根据偶函数的定义可判断选项A为偶函数,而根据反比例函数在定义域上的单调性知B在定义域上没有单调性,根据减函数的定义可以判断出C在(0,1)上为减函数,这便可判断A,B,C这三个选项错误,而根据奇函数的定义及二次函数、分段函数的单调性可判断D正确.
解答 解:A.y=-x2为偶函数,∴该选项错误;
B.$y=\frac{-1}{x}$在定义域上没有单调性,∴该选项错误;
C.$y=x+\frac{1}{x}$,x∈(0,1)时,x增大时,$\frac{1}{x}$的减小幅度大于x的增大幅度,从而y减小;
∴该函数在(0,1)上为减函数,∴该选项错误;
D.y=x|x|=$\left\{\begin{array}{l}{{x}^{2}}&{x≥0}\\{-{x}^{2}}&{x<0}\end{array}\right.$,显然该函数为奇函数;
x≥0时,y=x2为增函数,x<0时,y=-x2为增函数,且x2>-x2;
∴该函数在R上为增函数,即该选项正确.
故选D.
点评 考查奇函数、偶函数的定义,反比例函数在定义域上没有单调性,减函数的定义,含绝对值函数的处理方法:去绝对值号,二次函数的单调性的判断,分段函数单调性的判断.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.若A={2,3,4},B={x|x<4},则集合A∩B中的元素个数是( )
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
18.已知函数$f(x)=a-\frac{4}{{{2^x}+1}}({a∈R})$是定义在(-∞,+∞)上的奇函数.
(1)求a的值,并写出函数f(x)的解析式;
(2)求证:函数f(x)在上是增函数.
(1)求a的值,并写出函数f(x)的解析式;
(2)求证:函数f(x)在上是增函数.
5.“抛物线y=ax2的准线方程为y=2”是“抛物线y=ax2的焦点与双曲线$\frac{y^2}{3}-{x^2}=1$的焦点重合”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.下列选项中是函数f(x)=sinx-$\sqrt{3}$cosx的零点的是( )
| A. | $\frac{π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{7π}{6}$ | D. | $\frac{4π}{3}$ |
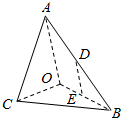 如图,在三棱锥AB0C中.AO⊥平面BOC,∠OAB=∠OAC=$\frac{π}{6}$.AB=AC=2.BC=$\sqrt{2}$,D,E分别为AB,OB的中点.
如图,在三棱锥AB0C中.AO⊥平面BOC,∠OAB=∠OAC=$\frac{π}{6}$.AB=AC=2.BC=$\sqrt{2}$,D,E分别为AB,OB的中点.