题目内容
已知函数f(x)=loga(1-x)+loga(x+3),其中a>0且a≠1.
(Ⅰ)求函数f(x)的定义域;
(Ⅱ)求函数f(x)的零点;
(Ⅲ)若函数f(x)的最大值为2,求a的值.
(Ⅰ)求函数f(x)的定义域;
(Ⅱ)求函数f(x)的零点;
(Ⅲ)若函数f(x)的最大值为2,求a的值.
考点:函数的最值及其几何意义,函数的定义域及其求法,函数的零点
专题:计算题,函数的性质及应用
分析:(Ⅰ)由题意,
,从而求函数f(x)的定义域;
(Ⅱ)函数的零点即方程loga(1-x)(x+3)=0的解,从而求函数f(x)的零点;
(Ⅲ)由f(x)=loga(1-x)(x+3)的最大值为2可得f(-1)=loga(1+1)(-1+3)=loga4=2,从而求a的值.
|
(Ⅱ)函数的零点即方程loga(1-x)(x+3)=0的解,从而求函数f(x)的零点;
(Ⅲ)由f(x)=loga(1-x)(x+3)的最大值为2可得f(-1)=loga(1+1)(-1+3)=loga4=2,从而求a的值.
解答:
解:(Ⅰ)由题意得,
,
解得,-3<x<1,
即函数f(x)的定义域为(-3,1);
(Ⅱ)f(x)=loga(1-x)+loga(x+3)=loga(1-x)(x+3),
令loga(1-x)(x+3)=0,
则(1-x)(x+3)=1,
则x=
-1,x=-
-1;
即函数f(x)的零点为
-1,-
-1;
(Ⅲ)∵f(x)=loga(1-x)(x+3)的最大值为2,
∴f(-1)=loga(1+1)(-1+3)=loga4=2,
则a=2.
|
解得,-3<x<1,
即函数f(x)的定义域为(-3,1);
(Ⅱ)f(x)=loga(1-x)+loga(x+3)=loga(1-x)(x+3),
令loga(1-x)(x+3)=0,
则(1-x)(x+3)=1,
则x=
| 3 |
| 3 |
即函数f(x)的零点为
| 3 |
| 3 |
(Ⅲ)∵f(x)=loga(1-x)(x+3)的最大值为2,
∴f(-1)=loga(1+1)(-1+3)=loga4=2,
则a=2.
点评:本题考查了函数的定义域,零点及最值的求法,函数的零点转化为方程的根,属于中档题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
如图是计算t=12×22×…×i2的程序,程序中循环体执行的次数为( )


| A、3 | B、4 | C、5 | D、6 |
定义在R上的偶函数f (x)满足:对任意的x1,x2∈[0,+∞)(x1≠x2),有
<0,又f (-3)=1,则不等式f (x)<1的解集为( )
| f(x2)-f(x1) |
| x2-x1 |
| A、{x|x<-3或x>3} |
| B、{x|x<-3或0<x<3} |
| C、{x|x>3或-3<x<0} |
| D、{x|-3<x<0或0<x<3} |
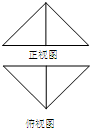 把边长为1的正方形ABCD沿对角线BD折起,连结AC,得到三棱锥C-ABD,其正视图与俯视图均为全等的等腰直角三角形,如图所示,则侧视图的面积为( )
把边长为1的正方形ABCD沿对角线BD折起,连结AC,得到三棱锥C-ABD,其正视图与俯视图均为全等的等腰直角三角形,如图所示,则侧视图的面积为( )