题目内容
已知|
|=6,|
|=3,
•
=-12,则向量
在向量
方向上的投影是 .
| a |
| b |
| a |
| b |
| a |
| b |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:根据投影的定义,先求向量
,
夹角的余弦值,投影就很容易求出.
| a |
| b |
解答:
解:设θ是向量
,
的夹角,则cosθ=
=-
,根据投影的定义,向量
在向量
方向的投影是:|
|cosθ=6×(-
)=-4.
故答案为:-4.
| a |
| b |
| ||||
|
|
| 2 |
| 3 |
| a |
| b |
| a |
| 2 |
| 3 |
故答案为:-4.
点评:考察一个向量在另一向量方向上投影的定义,比较容易求解.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
从0到9这10个数字中任取3个数字组成一个没有重复数字的三位数,则这个数能被3整除的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=
在区间[3,6]上的最大值、最小值分别是( )
| 4 |
| x-2 |
| A、4,1 | B、4,0 |
| C、1,0 | D、最大值4,无最小值 |
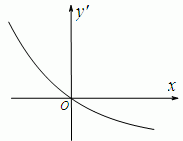 已知函数y=f(x)的导函数f′(x)的图象大致为如图,且f(15)=
已知函数y=f(x)的导函数f′(x)的图象大致为如图,且f(15)= 若aij表示n×n阶矩阵,如图所示中第i行、第j列的元素(i、j=1,2,3,…,n),其中若aij=321,则i+j=
若aij表示n×n阶矩阵,如图所示中第i行、第j列的元素(i、j=1,2,3,…,n),其中若aij=321,则i+j=