如图.阴影部分是由四个全等的直角三角形组成的图形.若直角三角形两条直角边的长分别为a.b.且a=2b.则在大正方形内随即掷一点.这一点落在正方形内的概率为$\frac{1}{5}$．题目和参考答案——青夏教育精英家教网—

题目内容

17．

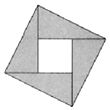如图，阴影部分是由四个全等的直角三角形组成的图形，若直角三角形两条直角边的长分别为a，b，且a=2b，则在大正方形内随即掷一点，这一点落在正方形内的概率为$\frac{1}{5}$．

分析求出三角形的面积，再求出大正方形的面积，根据比值解得即可．

解答解：由题意，大正方形面积为a²+b²=5b²，
三角形的面积为$\frac{1}{2}$ab=b²，
∴小正方形面积为b²，
∴在大正方形内随即掷一点，这一点落在正方形内的概率为$\frac{1}{5}$
故答案为$\frac{1}{5}$．

点评本题考查几何概型的求法：首先根据题意将代数关系用面积表示出来，一般用阴影区域表示所求事件（A）；然后计算阴影区域的面积和总面积的比，这个比即事件（A）发生的概率．

练习册系列答案

$\frac{{\sqrt{2}}}{2}$

$\frac{{3\sqrt{2}}}{2}$

8．已知F为双曲线$C：\frac{x^2}{4}-\frac{y^2}{2}=1$的一个焦点，则点F到双曲线C的一条渐近线的距离为$\sqrt{2}$．

	A．	线性正相关关系
	B．	由回归方程无法判断其正负相关关系
	C．	线性负相关关系
	D．	不存在线性相关关系

12．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足：|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1，且$\overrightarrow{a}•\overrightarrow{b}=\frac{1}{2}$，若$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$，其中x＞0，y＞0且x+y=2，则|$\overrightarrow{c}$|最小值是$\sqrt{3}$．

2．已知命题P：?x∈（-∞，0），2^x＜3^x；命题q：?x∈（0，π），sinx≤1，则下列命题为真命题的是（　　）

9．

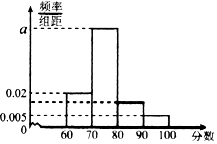某校对高二年级选学生物的学生的某次测试成绩进行了统计，随机抽取了m名学生的成绩作为样本，根据此数据作出了频率分布统计表和频率分布直方图如下：

分组	频数	频率
[60，70）	16	0.2
[70，80）	50	n
[80，90）	10	P
[90，100]	4	0.05
合计	M	I

（I）求表中n，p的值和频率分布直方图中a的值；
（II）如果用分层抽样的方法，从样本成绩在[60，70]和[90，100]的学生中共抽取5人，再从5人中选2人，求这2人成绩在[60，70]的概率．

6．已知$a=\frac{2}{5}$，$b={2^{\frac{1}{2}}}$，$c=log_3^{\frac{1}{2}}$，则（　　）

7．在一次比赛中某队共有甲，乙，丙等5位选手参加，赛前用抽签的方法决定出场的顺序，则乙、丙都不与甲相邻出场的概率是（　　）

试题分类