题目内容
6.已知$a=\frac{2}{5}$,$b={2^{\frac{1}{2}}}$,$c=log_3^{\frac{1}{2}}$,则( )| A. | b>c>a | B. | c>b>a | C. | b>a>c | D. | a>b>c |
分析 $a=\frac{2}{5}$=0.4,$b={2^{\frac{1}{2}}}$=$\sqrt{2}$>1,$c=log_3^{\frac{1}{2}}$<0,即可得出.
解答 解:$a=\frac{2}{5}$=0.4,$b={2^{\frac{1}{2}}}$=$\sqrt{2}$>1,$c=log_3^{\frac{1}{2}}$<0,
则b>a>c.
故选:C.
点评 本题查了函数的单调性,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
14.已知m为实数,i为虚数单位,若m+(m2-4)i>0,则$\frac{m+2i}{2-2i}$=( )
| A. | i | B. | 1 | C. | -i | D. | -1 |
11.过函数$f(x)=\frac{1}{3}{x^3}-{x^2}$图象上一个动点作函数的切线,则切线倾斜角的范围为( )
| A. | $[0,\frac{3π}{4}]$ | B. | $[0,\frac{π}{2})∪[\frac{3π}{4},π)$ | C. | $[\frac{3π}{4},π)$ | D. | $(\frac{π}{2},\frac{3π}{4}]$ |
15.已知集合M={x|x≥-1},N={x|-2<x<2},则M∩N=( )
| A. | (-∞,-1] | B. | [-1,2) | C. | (-1,2] | D. | (2,+∞) |
16.在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的上下顶点分别为A,B,右顶点为C,右焦点为F,延长BF与AC交于点P,若O,F,P,A四点共圆,则该椭圆的离心率为( )
| A. | $\frac{{\sqrt{2}-1}}{2}$ | B. | $\frac{{\sqrt{3}-1}}{2}$ | C. | $\frac{{\sqrt{5}-1}}{2}$ | D. | $\frac{{\sqrt{5}-\sqrt{2}}}{2}$ |
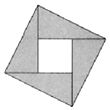 如图,阴影部分是由四个全等的直角三角形组成的图形,若直角三角形两条直角边的长分别为a,b,且a=2b,则在大正方形内随即掷一点,这一点落在正方形内的概率为$\frac{1}{5}$.
如图,阴影部分是由四个全等的直角三角形组成的图形,若直角三角形两条直角边的长分别为a,b,且a=2b,则在大正方形内随即掷一点,这一点落在正方形内的概率为$\frac{1}{5}$.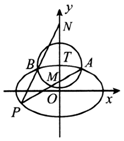 如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,以椭圆C的上顶点T为圆心作圆T:x2+(y-1)2=r2(r>0),圆T与椭圆C在第一象限交于点A,在第二象限交于点B.
如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,以椭圆C的上顶点T为圆心作圆T:x2+(y-1)2=r2(r>0),圆T与椭圆C在第一象限交于点A,在第二象限交于点B.