题目内容
9.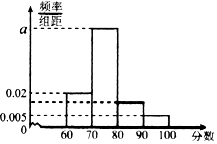 某校对高二年级选学生物的学生的某次测试成绩进行了统计,随机抽取了m名学生的成绩作为样本,根据此数据作出了频率分布统计表和频率分布直方图如下:
某校对高二年级选学生物的学生的某次测试成绩进行了统计,随机抽取了m名学生的成绩作为样本,根据此数据作出了频率分布统计表和频率分布直方图如下:| 分组 | 频数 | 频率 |
| [60,70) | 16 | 0.2 |
| [70,80) | 50 | n |
| [80,90) | 10 | P |
| [90,100] | 4 | 0.05 |
| 合计 | M | I |
(II)如果用分层抽样的方法,从样本成绩在[60,70]和[90,100]的学生中共抽取5人,再从5人中选2人,求这2人成绩在[60,70]的概率.
分析 (Ⅰ)由频率=$\frac{频数}{总数}$,结合频率分布表和频率分布直方图,能求出表中n,p的值和频率分布直方图中a的值.
(Ⅱ)样本分数在[60,70)中的有16人,在[90,100)中的有4人,用分层抽样的方法,从样本成绩在[60,70]和[90,100]的学生中共抽取5人,则[60,70)中抽取4人,[90,100)中抽取1人,由此能求出结果.
解答 解:(Ⅰ)由题意$\frac{16}{m}=0.2$,解得m=80,
∴n=$\frac{50}{80}=0.625$,
∴p=1-0.2-0.625-0.05=0.125.
∴a=$\frac{n}{10}$=$\frac{0.625}{10}$=0.0625.
(Ⅱ)样本分数在[60,70)中的有0.02×10×80=16人,
在[90,100)中的有0.005×10×80=4人,
用分层抽样的方法,从样本成绩在[60,70]和[90,100]的学生中共抽取5人,
则[60,70)中抽取$\frac{16}{20}×5$=4人,[90,100)中抽取$\frac{4}{20}×5$=1人,
再从5人中选2人,基本事件总数n=${C}_{5}^{2}=10$,
这2人成绩在[60,70)包含的基本事件个数m=${C}_{4}^{2}$=6,
这2人成绩在[60,70]的概率p=$\frac{m}{n}=\frac{6}{10}$=0.6.
点评 本题考查频率分布表、频率分布直方图、分层抽样的应用,考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.若函数$f(x)=\sqrt{3}sin(2x+φ)+cos(2x+φ)(|φ|<\frac{π}{2})$为偶函数,则( )
| A. | f(x)的最小正周期为π,且在$(0,\frac{π}{2})$上为增函数 | |
| B. | f(x)的最小正周期为$\frac{π}{2}$,且在$(0,\frac{π}{4})$上为增函数 | |
| C. | f(x)的最小正周期为$\frac{π}{2}$,且在$(0,\frac{π}{4})$上为减函数 | |
| D. | f(x)的最小正周期为π,且在$(0,\frac{π}{2})$上为减函数 |
14.已知m为实数,i为虚数单位,若m+(m2-4)i>0,则$\frac{m+2i}{2-2i}$=( )
| A. | i | B. | 1 | C. | -i | D. | -1 |
19.一个几何体的三视图如图所示,则其体积为( )


| A. | π+2 | B. | 2π+4 | C. | π+4 | D. | 2π+2 |
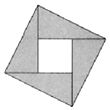 如图,阴影部分是由四个全等的直角三角形组成的图形,若直角三角形两条直角边的长分别为a,b,且a=2b,则在大正方形内随即掷一点,这一点落在正方形内的概率为$\frac{1}{5}$.
如图,阴影部分是由四个全等的直角三角形组成的图形,若直角三角形两条直角边的长分别为a,b,且a=2b,则在大正方形内随即掷一点,这一点落在正方形内的概率为$\frac{1}{5}$.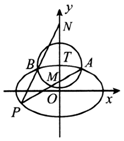 如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,以椭圆C的上顶点T为圆心作圆T:x2+(y-1)2=r2(r>0),圆T与椭圆C在第一象限交于点A,在第二象限交于点B.
如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,以椭圆C的上顶点T为圆心作圆T:x2+(y-1)2=r2(r>0),圆T与椭圆C在第一象限交于点A,在第二象限交于点B.