题目内容
8.已知F为双曲线$C:\frac{x^2}{4}-\frac{y^2}{2}=1$的一个焦点,则点F到双曲线C的一条渐近线的距离为$\sqrt{2}$.分析 根据题意,由双曲线的标准方程可得a、b的值,由双曲线的几何性质可得焦点坐标以及渐近线的方程,进而由点到直线的距离公式计算可得答案.
解答 解:根据题意,双曲线的方程为:$\frac{x^2}{4}-\frac{y^2}{2}=1$,
其中a=$\sqrt{4}$=2,b=$\sqrt{2}$,
则有c=$\sqrt{4+2}$=$\sqrt{6}$,故焦点坐标为(±$\sqrt{6}$,0),
其渐近线方程为:y=±$\frac{\sqrt{2}}{2}$x,
设F($\sqrt{6}$,0),到渐近线y=$\frac{\sqrt{2}}{2}$x的距离d=$\frac{|\frac{\sqrt{2}}{2}×\sqrt{6}|}{\sqrt{1+\frac{1}{2}}}$=$\sqrt{2}$,
故答案为:$\sqrt{2}$.
点评 本题考查双曲线的几何性质,关键是利用双曲线的标准方程,计算出焦点坐标以及渐近线的方程.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
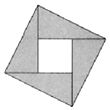 如图,阴影部分是由四个全等的直角三角形组成的图形,若直角三角形两条直角边的长分别为a,b,且a=2b,则在大正方形内随即掷一点,这一点落在正方形内的概率为$\frac{1}{5}$.
如图,阴影部分是由四个全等的直角三角形组成的图形,若直角三角形两条直角边的长分别为a,b,且a=2b,则在大正方形内随即掷一点,这一点落在正方形内的概率为$\frac{1}{5}$.