题目内容
2.已知命题P:?x∈(-∞,0),2x<3x;命题q:?x∈(0,π),sinx≤1,则下列命题为真命题的是( )| A. | p∧q | B. | p∨(¬q) | C. | p∧(¬q) | D. | (¬p)∧q |
分析 先分析命题p,q的真假,进而根据复合命题真假判断的真值表,可得答案.
解答 解:∵当x∈(-∞,0)时,2x>3x恒成立,
故命题P:?x∈(-∞,0),2x<3x为假命题;
当x∈(0,π)时,0<sinx≤1,
故命题q为真命题,
故命题p∧q,p∨(¬q),p∧(¬q)均为假命题;
(¬p)∧q为真命题,
故选:D
点评 本题以命题的真假判断与应用为载体,考查了复合命题,函数的图象和性质,难度中档.

练习册系列答案
相关题目
14.已知m为实数,i为虚数单位,若m+(m2-4)i>0,则$\frac{m+2i}{2-2i}$=( )
| A. | i | B. | 1 | C. | -i | D. | -1 |
11.过函数$f(x)=\frac{1}{3}{x^3}-{x^2}$图象上一个动点作函数的切线,则切线倾斜角的范围为( )
| A. | $[0,\frac{3π}{4}]$ | B. | $[0,\frac{π}{2})∪[\frac{3π}{4},π)$ | C. | $[\frac{3π}{4},π)$ | D. | $(\frac{π}{2},\frac{3π}{4}]$ |
12.圆x2+y2-4x+6y=0的圆心坐标是( )
| A. | (2,3) | B. | (-2,3) | C. | (-2,-3) | D. | (2,-3) |
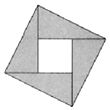 如图,阴影部分是由四个全等的直角三角形组成的图形,若直角三角形两条直角边的长分别为a,b,且a=2b,则在大正方形内随即掷一点,这一点落在正方形内的概率为$\frac{1}{5}$.
如图,阴影部分是由四个全等的直角三角形组成的图形,若直角三角形两条直角边的长分别为a,b,且a=2b,则在大正方形内随即掷一点,这一点落在正方形内的概率为$\frac{1}{5}$. 某程序框图如图所示,若运行该程序后输出S为$\frac{5}{6}$.
某程序框图如图所示,若运行该程序后输出S为$\frac{5}{6}$.