题目内容
已知函数f(x)=2tan(ωx+
)(ω＞0)的最小正周期为
．
（Ⅰ）求函数f（x）的定义域；
（Ⅱ）求函数f（x）的单调区间．
| π |
| 3 |
| π |
| 2 |
（Ⅰ）求函数f（x）的定义域；
（Ⅱ）求函数f（x）的单调区间．
考点：三角函数的周期性及其求法,函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：（Ⅰ）根据正切函数的周期公式求出函数的表达式，即可求函数f（x）的定义域；
（Ⅱ）根据正切函数的单调性即可求函数f（x）的单调区间．
（Ⅱ）根据正切函数的单调性即可求函数f（x）的单调区间．
解答：
解：（Ⅰ）由已知，
=
，ω=2，
所以f(x)=2tan(2x+
)，
由2x+
≠kπ+
，解得x≠
+
，
所以函数的定义域为{x|x≠
+
， k∈Z}．
（Ⅱ）由kπ-
＜2x+
＜kπ+
，
解得
-
＜x＜
+
，
所以函数f（x）的单调递增区间为(
-
，
+
)，其中k∈Z．
| π |
| ω |
| π |
| 2 |
所以f(x)=2tan(2x+
| π |
| 3 |
由2x+
| π |
| 3 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 12 |
所以函数的定义域为{x|x≠
| kπ |
| 2 |
| π |
| 12 |
（Ⅱ）由kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
解得
| kπ |
| 2 |
| 5π |
| 12 |
| kπ |
| 2 |
| π |
| 12 |
所以函数f（x）的单调递增区间为(
| kπ |
| 2 |
| 5π |
| 12 |
| kπ |
| 2 |
| π |
| 12 |
点评：本题主要考查正切函数的图象和性质，要求熟练掌握正切函数的周期公式，和单调性的性质．
练习册系列答案
备战中考寒假系列答案
相关题目
在数列{an}中，an+1=
（n∈N+）且a7=
，则a5=（ ）
| 2an |
| 2+an |
| 1 |
| 2 |
| A、1 | ||
B、
| ||
C、
| ||
| D、-1 |
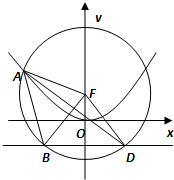设抛物线C：x2=2py（p＞0）的焦点为F，准线为l，A为C上一点，已知以F为圆心，FA为半径的圆F交l于B，D两点．若∠BFD=90°，△ABD的面积为4
如图，直三棱柱ABC-A1B1C1中，点D是BC上一点．