题目内容
已知f(2x+1)=x2,则f′(x)= .
考点:导数的运算
专题:导数的综合应用
分析:令t=2x+1,解得x=
,由f(2x+1)=x2可化为f(t)=(
)2,即f(x)=
,再利用导数的右上方在即可得出.
| t-1 |
| 2 |
| t-1 |
| 2 |
| (x-1)2 |
| 4 |
解答:
解:令t=2x+1,解得x=
,
∴f(2x+1)=x2可化为f(t)=(
)2,
即f(x)=
,∴f′(x)=
.
故答案为:
.
| t-1 |
| 2 |
∴f(2x+1)=x2可化为f(t)=(
| t-1 |
| 2 |
即f(x)=
| (x-1)2 |
| 4 |
| x-1 |
| 2 |
故答案为:
| x-1 |
| 2 |
点评:本题考查了通过换元求函数的导数,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
方程x2+y2-2x+4y+1=0所表示的图形的面积是( )
| A、π | ||
| B、2π | ||
| C、4π | ||
D、
|
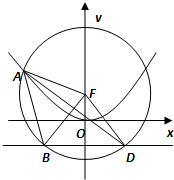 设抛物线C:x2=2py(p>0)的焦点为F,准线为l,A为C上一点,已知以F为圆心,FA为半径的圆F交l于B,D两点.若∠BFD=90°,△ABD的面积为4
设抛物线C:x2=2py(p>0)的焦点为F,准线为l,A为C上一点,已知以F为圆心,FA为半径的圆F交l于B,D两点.若∠BFD=90°,△ABD的面积为4 如图,直三棱柱ABC-A1B1C1中,点D是BC上一点.
如图,直三棱柱ABC-A1B1C1中,点D是BC上一点.