题目内容
设函数f(x)定义在(0,+∞)上,其图象经过点M(1,0),导函数f′(x)=x-1,g(x)=f(x)+f′(x).
(1)如果不等式m≥g(x)有解,求实数m的取值范围;
(2)如果N(t,b)是函数y=f′(x)图象上一点,证明:当0<t<1,g(t)>g(b);
(3)是否存在x0>1,使得lnx<g(x0)<lnx+
对任意x>0恒成立?若存在,求出x0 的取值范围;若不存在,请说明理由.
(1)如果不等式m≥g(x)有解,求实数m的取值范围;
(2)如果N(t,b)是函数y=f′(x)图象上一点,证明:当0<t<1,g(t)>g(b);
(3)是否存在x0>1,使得lnx<g(x0)<lnx+
| 2 |
| x |
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的极值
专题:导数的综合应用
分析:(1)由图象经过点M(1,0),导函数f′(x)=x-1,求出f(x),g(x)的解析式,不等式m≥g(x)有解,就是m大于等g(x)的最大值,利用g(x)的单调性求出g(x)的最大值,从而求出m的取值范围;
(2)构造函数h(t)=g(t)-g(b),利用h(t)的单调性求出h(t)的最值,从而证明不等式;
(3)利用反证法,假设结论不成立,取x1=eg(x0)时,得出矛盾,从而得证.
(2)构造函数h(t)=g(t)-g(b),利用h(t)的单调性求出h(t)的最值,从而证明不等式;
(3)利用反证法,假设结论不成立,取x1=eg(x0)时,得出矛盾,从而得证.
解答:
解:(1)∵f′(x)=
,∴f(x)=lnx+c(c为常数),
又∵f(1)=0,∴ln1+c=0,即c=0,∴f(x)=lnx,g(x)=lnx+
,
∴g′(x)=
,令g′(x)=0,即
=0,解得x=1,
当x∈(0,1)时,g′(x)<0时,当x∈(1,+∞)时,g′(x)>0.
所以x=1是函数g(x)在(0,+∞)上的唯一极小值点,从而是最小值点,…(4分)
所以g(x)的最小值是g(1)=1.“不等式m≥g(x)有解”的等价命题是“m≥[g(x)]min”,故m≥1.
(2)证明:点N(t,b)是函数y=f′(x)图象上一点,
b=f′(t)=
,g(b)=g(
)=-lnt+t.
设h(t)=g(t)-g(b)=g(t)-g(
)=2lnt-t+
,则h′(t)=t-
,
当t∈(0,1)时,h(t)<0,此时h(t)=2lnt-t+
是减函数,故h(t)>h(1),
又t=1时,h(1)=0,即h(t)>0,也就是2lnt-t+
>0,∴g(t)>g(
).
故当t∈(0,1)时,g(t)>g(b).
(3)满足条件的x0不存在.证明如下:
假设存在x0>0得对任意x>0有lnx<g(x0)<lnx+
①,
但对上述的x0,取x1=eg(x0)时,有lnx1=g(x0),这与①左边的不等式矛盾,
因此不存在x0,使lnx<g(x0)<lnx+
对任意x>0成立.
| 1 |
| x |
又∵f(1)=0,∴ln1+c=0,即c=0,∴f(x)=lnx,g(x)=lnx+
| 1 |
| x |
∴g′(x)=
| x-1 |
| x2 |
| x-1 |
| x2 |
当x∈(0,1)时,g′(x)<0时,当x∈(1,+∞)时,g′(x)>0.
所以x=1是函数g(x)在(0,+∞)上的唯一极小值点,从而是最小值点,…(4分)
所以g(x)的最小值是g(1)=1.“不等式m≥g(x)有解”的等价命题是“m≥[g(x)]min”,故m≥1.
(2)证明:点N(t,b)是函数y=f′(x)图象上一点,
b=f′(t)=
| 1 |
| t |
| 1 |
| t |
设h(t)=g(t)-g(b)=g(t)-g(
| 1 |
| t |
| 1 |
| t |
| (t-1)2 |
| t2 |
当t∈(0,1)时,h(t)<0,此时h(t)=2lnt-t+
| 1 |
| t |
又t=1时,h(1)=0,即h(t)>0,也就是2lnt-t+
| 1 |
| t |
| 1 |
| t |
故当t∈(0,1)时,g(t)>g(b).
(3)满足条件的x0不存在.证明如下:
假设存在x0>0得对任意x>0有lnx<g(x0)<lnx+
| 2 |
| x |
但对上述的x0,取x1=eg(x0)时,有lnx1=g(x0),这与①左边的不等式矛盾,
因此不存在x0,使lnx<g(x0)<lnx+
| 2 |
| x |
点评:本题目考查了,求解析式,等价转化,分类讨论,反证法,以及化归思想,是一道导数的综合题目,有一定的难度.

练习册系列答案
相关题目
函数y=sinα+cosα的图象的一个对称中心是( )
A、(
| ||||
B、(
| ||||
C、(-
| ||||
D、(
|
已知定义在R上的函数y=f(x)满足下列三个条件:
①对于任意的x∈R,都有f(x+4)=f(x);
②对于任意的0≤x1≤x2≤2,都有f(x1)<f(x2);
③函数y=f(x+2)是偶函数;
则下列结论中正确的是( )
①对于任意的x∈R,都有f(x+4)=f(x);
②对于任意的0≤x1≤x2≤2,都有f(x1)<f(x2);
③函数y=f(x+2)是偶函数;
则下列结论中正确的是( )
| A、f(6.5)<f(5)<f(15.5) |
| B、f(5)<f(6.5)<f(15.5) |
| C、f(5)<f(15.5)<f(6.5) |
| D、f(15.5)<f(5)<f(6.5) |
函数y=cosx(sinx+
cosx)-
的图象( )
| 3 |
| ||
| 2 |
A、关于点(
| ||
B、关于直线x=
| ||
C、关于点(
| ||
D、关于直线x=
|
若?a∈(0,+∞),?θ∈R使asinθ≥a成立,则cos(θ-
)的值为( )
| π |
| 6 |
A、
| ||||
B、
| ||||
C、±
| ||||
D、±
|
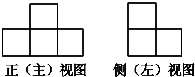 用小正方体搭成一个几何体,如图是它的正(主)视图和侧(左)视图,搭成这个几何体的小正方体最多为
用小正方体搭成一个几何体,如图是它的正(主)视图和侧(左)视图,搭成这个几何体的小正方体最多为