题目内容
17.某精密仪器生产有两道相互独立的先后工序,每道工序都要经过相互独立的工序检查,且当第一道工序检查合格后才能进入第二道工序,两道工序都合格,产品才完全合格,.经长期监测发现,该仪器第一道工序检查合格的概率为$\frac{8}{9}$,第二道工序检查合格的概率为$\frac{9}{10}$,已知该厂三个生产小组分别每月负责生产一台这种仪器.(I)求本月恰有两台仪器完全合格的概率;
(Ⅱ)若生产一台仪器合格可盈利5万元,不合格则要亏损1万元,记该厂每月的赢利额为ξ,求ξ的分布列和每月的盈利期望.
分析 (I)求出每生产一台合格仪器的概率,利用独立重复试验的概率公式求本月恰有两台仪器完全合格的概率;
(II)根据题意得到变量的可能的取值,根据变量对应的事件,利用独立重复试验的概率公式得到概率,写出分布列,根据做出的变量的分布列,代入求期望值的公式做出期望值
解答 解:(Ⅰ) 设恰有两台仪器完全合格的事件为A,每台仪器经两道工序检验完全合格的概率为$P=\frac{8}{9}×\frac{9}{10}{=}\frac{4}{5}$…(2分)
所以$P(A)={C_3}^2{p^2}(1-p)={C_3}^2{(\frac{4}{5})^2}(1-\frac{4}{5})=\frac{48}{125}$…(5分)
(Ⅱ) 每月生产的仪器完全合格的台数可为3,2,1,0四种
所以赢利额ξ的数额可以为15,9,3,-3…(7分)
当ξ=15时,$P(ξ=15)={C_3}^3{(\frac{4}{5})^3}=\frac{64}{125}$
当ξ=9时,$P(ξ=9)={C_3}^2{(\frac{4}{5})^2}\frac{1}{5}=\frac{48}{125}$
当ξ=3时,$P(ξ=3)={C_3}^1\frac{4}{5}{(\frac{1}{5})^2}=\frac{12}{125}$
当ξ=-3时,$P(ξ=-3)={C_3}^0{(\frac{1}{5})^3}=\frac{1}{125}$…(10分)
每月的盈利期望$Eξ=15×\frac{64}{125}+9×\frac{48}{125}+3×\frac{12}{125}+(-3)\frac{1}{125}=\frac{57}{5}=10.14$
所以每月的盈利期望值为10.14万元…(12分)
点评 本题考查离散型随机变量的分布列和期望,独立重复试验的概率公式,本题解题的关键是看出所给的变量符合什么规律,利用概率的公式来解题.

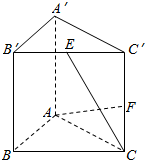 在直三棱柱ABC-A′B′C′中,AB=AC=2,AA′=3,AB⊥AC,E为棱B′C′的中点,F为侧棱CC′上一点,若CE⊥AF,则AF与平面ABB′A′所成的角的正切值为( )
在直三棱柱ABC-A′B′C′中,AB=AC=2,AA′=3,AB⊥AC,E为棱B′C′的中点,F为侧棱CC′上一点,若CE⊥AF,则AF与平面ABB′A′所成的角的正切值为( )| A. | 3 | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{4}{3}$ |
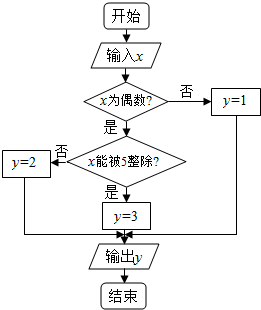 某算法的程序框图如图所示,其中输入的变量J在1,2,3,…,30这30个整数中等可能随机产生.
某算法的程序框图如图所示,其中输入的变量J在1,2,3,…,30这30个整数中等可能随机产生.(1)分别求出(按程序框图正确编程运行时)输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录
了输出y的值为i(i=1,2,3)的频数,下面是甲、乙所作频数统计表的部分数据:
甲的频数统计表(部分)
| 运行次数 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
| 30 | 16 | 11 | 3 |
| … | … | … | … |
| 2000 | 967 | 783 | 250 |
| 运行次数 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
| 30 | 13 | 13 | 4 |
| … | … | … | … |
| 2000 | 998 | 803 | 199 |
 在公比为2的等比数列{an}中,a2与a3的等差中项是9$\sqrt{3}$.
在公比为2的等比数列{an}中,a2与a3的等差中项是9$\sqrt{3}$.