Question

3．已知函数f（x）=$\left\{\begin{array}{l}{{2}^{x}+1，x≤0}\\{|lo{g}_{2}x|，x＞0}\end{array}\right.$，g（x）=[f（x）]²-af（x），若函数g（x）存在四个零点，则实数a的取值范围为（1，2]．

Answer 1

分析 画出函数f（x）=$\left\{\begin{array}{l}{{2}^{x}+1，x≤0}\\{|lo{g}_{2}x|，x＞0}\end{array}\right.$的图象，令g（x）=0，则f（x）=0，或f（x）=a，进而将函数g（x）存在四个零点，转化为f（x）=a有三根，数形结合可得答案．

解答 解：函数f（x）=$\left\{\begin{array}{l}{{2}^{x}+1，x≤0}\\{|lo{g}_{2}x|，x＞0}\end{array}\right.$的图象如下图所示：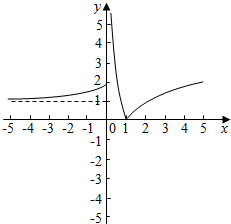

若g（x）=[f（x）]²-af（x）=0，则f（x）=0，或f（x）=a，
由函数图象可得f（x）=0有一解，
则f（x）=a有3解，
故a∈（1，2]，
故答案为：（1，2]

点评 本题考查的知识点是分段函数的应用，数形结合思想，难度中档．