题目内容
1．已知曲线C的参数方程是$\left\{\begin{array}{l}{x=cosα}\\{y=m+sinα}\end{array}\right.$（α为参数），直线l的参数方程为$\left\{\begin{array}{l}{x=1+\frac{\sqrt{5}}{5}t}\\{y=4+\frac{2\sqrt{5}}{5}t}\end{array}\right.$（t为参数），（1）求曲线C与直线l的普通方程；
（2）若直线l与曲线C相交于P，Q两点，且|PQ|=$\frac{4\sqrt{5}}{5}$，求实数m的值．
分析 （1）由sin2α+cos2α=1，能求出曲线C的普通方程，消去直线l中的参数，能求出直线l的普通方程．．
（2）求出圆心C（0，m）到直线l：2x-y+2=0的距离d，再由勾股定理结合弦长能求出m．
解答 解：（1）∵曲线C的参数方程是$\left\{\begin{array}{l}{x=cosα}\\{y=m+sinα}\end{array}\right.$（α为参数），
∴曲线C的普通方程：x2+（y-m）2=1，
∵直线l的参数方程为$\left\{\begin{array}{l}{x=1+\frac{\sqrt{5}}{5}t}\\{y=4+\frac{2\sqrt{5}}{5}t}\end{array}\right.$（t为参数），
∴消去参数，得直线l的普通方程为：2x-y+2=0．
（2）∵曲线C：x2+（y-m）2=1是以C（0，m）为圆心，以1为半径的圆，
圆心C（0，m）到直线l：2x-y+2=0的距离：d=$\frac{|0-m+2|}{\sqrt{4+1}}$=$\frac{\sqrt{5}}{5}$|m-2|，
又直线l与曲线C相交于P，Q两点，且|PQ|=$\frac{4\sqrt{5}}{5}$，
∴2$\sqrt{1-（\frac{\sqrt{5}}{5}|m-2|）^{2}}$=$\frac{4\sqrt{5}}{5}$
解得m=1或m=3．
点评 本题考查参数方程、普通方程的互化，考查实数值的求法，是中档题，解题时要认真审题，注意圆的性质、点到直线距离公式、勾股定理的合理运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
4．已知A、B是半径为R的球O的球面上两点，∠AOB=α，C为球面上的动点，若三棱锥O-ABC的体积最大，则α和最大体积分别为（ ）
| A． | $\frac{π}{3}$，$\frac{1}{6}$R3 | B． | $\frac{π}{3}$，$\frac{1}{3}$R3 | C． | $\frac{π}{2}$，$\frac{1}{3}$R3 | D． | $\frac{π}{2}$，$\frac{1}{6}$R3 |
6．若实数a，b在区间[0，$\sqrt{2}$]上取值，则函数f（x）=$\frac{2}{3}$ax3+bx2+ax在R上有两个相异极值点的概率是（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{\sqrt{2}}{4}$ | C． | $\frac{\sqrt{2}}{8}$ | D． | $\frac{1}{2}$ |
13．一几何体的三视图如图所示，则该几何体的表面积为（ ）
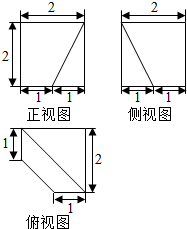
| A． | 20 | B． | 24 | C． | 16 | D． | $16+\frac{3}{2}\sqrt{10}$ |