题目内容
12.把函数y=3sin($\frac{1}{2}$x+$\frac{π}{6}$)的图象向右平移φ(φ>0)个单位,所的函数图象关于y轴对称,则φ的最小值为$\frac{4π}{3}$.分析 由函数图象变换可得函数解析式为y=3sin($\frac{1}{2}$x+$\frac{π}{6}$-$\frac{1}{2}$φ),由图象的对称性可得$\frac{1}{2}$φ-$\frac{π}{6}$=kπ+$\frac{π}{2}$,解得φ给k取值可得.
解答 解:把函数y=3sin($\frac{1}{2}$x+$\frac{π}{6}$)的图象向右平移φ(φ>0)个单位,
得到y=3sin[$\frac{1}{2}$(x-φ)+$\frac{π}{6}$)]=3sin($\frac{1}{2}$x+$\frac{π}{6}$-$\frac{1}{2}$φ)的图象,
∵所的函数y=3sin($\frac{1}{2}$x+$\frac{π}{6}$-$\frac{1}{2}$φ)图象关于y轴对称,
∴$\frac{1}{2}$φ-$\frac{π}{6}$=kπ+$\frac{π}{2}$,解得φ=2kπ+$\frac{4π}{3}$,k∈Z,
∵φ>0,∴当k=0时,φ取最小值$\frac{4π}{3}$.
故答案为:$\frac{4π}{3}$
点评 本题考查三角函数图象变换和图象的性质,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.圆周上有6个点,任取3个点可以做一个三角形,可得到三角形的个数( )
| A. | 6 | B. | 12 | C. | 18 | D. | 20 |
4.已知A、B是半径为R的球O的球面上两点,∠AOB=α,C为球面上的动点,若三棱锥O-ABC的体积最大,则α和最大体积分别为( )
| A. | $\frac{π}{3}$,$\frac{1}{6}$R3 | B. | $\frac{π}{3}$,$\frac{1}{3}$R3 | C. | $\frac{π}{2}$,$\frac{1}{3}$R3 | D. | $\frac{π}{2}$,$\frac{1}{6}$R3 |
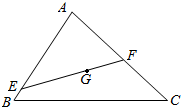 如图,G是△ABC的重心,过G的直线与边AB,AC分别相交于点E,F,若AE=mAB,AF=nAC(mn≠0),求$\frac{1}{m}$+$\frac{1}{n}$的值.
如图,G是△ABC的重心,过G的直线与边AB,AC分别相交于点E,F,若AE=mAB,AF=nAC(mn≠0),求$\frac{1}{m}$+$\frac{1}{n}$的值.