��Ŀ����
8����֪$\overrightarrow{a}$��$\overrightarrow{b}$��$\overrightarrow{c}$��ͬһƽ���ڵ���������������$\overrightarrow{a}$=��1��2������1����$\overrightarrow{c}$=��-2��k������$\overrightarrow{c}$��$\overrightarrow{a}$����$\overrightarrow{c}$�����ꣻ
��2����|$\overrightarrow{b}$|=$\frac{\sqrt{5}}{2}$����$\overrightarrow{a}$+2$\overrightarrow{b}$��2$\overrightarrow{a}$-$\overrightarrow{b}$��ֱ����$\overrightarrow{a}$��$\overrightarrow{b}$�ļнǦȣ�
���� ��1��������ƽ�е����ʣ������k��
��2����������ֱ�ã�$\overrightarrow{a}$+2$\overrightarrow{b}$��•��2$\overrightarrow{a}$-$\overrightarrow{b}$��=0���ɴ������$\overrightarrow{a}$��$\overrightarrow{b}$�ļнǦȣ�
��� �⣺��1����$\overrightarrow{a}$��$\overrightarrow{b}$��$\overrightarrow{c}$��ͬһƽ���ڵ�����������
$\overrightarrow{a}$=��1��2����$\overrightarrow{c}$=��-2��k������$\overrightarrow{c}$��$\overrightarrow{a}$��
��$\frac{-2}{1}=\frac{k}{2}$�����k=-4��
��$\overrightarrow{c}$��������-2��-4����
��2����|$\overrightarrow{b}$|=$\frac{\sqrt{5}}{2}$����$\overrightarrow{a}$+2$\overrightarrow{b}$��2$\overrightarrow{a}$-$\overrightarrow{b}$��ֱ��
�ࣨ$\overrightarrow{a}$+2$\overrightarrow{b}$��•��2$\overrightarrow{a}$-$\overrightarrow{b}$��=$2{\overrightarrow{a}}^{2}+3\overrightarrow{a}•\overrightarrow{b}-2{\overrightarrow{b}}^{2}$=0��
��2��5-3$\overrightarrow{a}•\overrightarrow{b}$-2��$\frac{5}{4}$=0��
��������$\overrightarrow{a}•\overrightarrow{b}$=-$\frac{5}{2}$��
��cos��=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=-1��
�ߦȡ�[0����]�����=�У�
���� ���⿼�����������꼰�������нǵ����ǻ����⣬����ʱҪ�������⣬ע��ƽ���������㷨��ĺ������ã�

| A�� | $\frac{\sqrt{2}}{2}$ | B�� | $\frac{\sqrt{2}}{4}$ | C�� | $\frac{\sqrt{2}}{8}$ | D�� | $\frac{1}{2}$ |
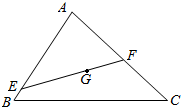 ��ͼ��G�ǡ�ABC�����ģ���G��ֱ�����AB��AC�ֱ��ཻ�ڵ�E��F����AE=mAB��AF=nAC��mn��0������$\frac{1}{m}$+$\frac{1}{n}$��ֵ��
��ͼ��G�ǡ�ABC�����ģ���G��ֱ�����AB��AC�ֱ��ཻ�ڵ�E��F����AE=mAB��AF=nAC��mn��0������$\frac{1}{m}$+$\frac{1}{n}$��ֵ��