题目内容
14.若log2$\sqrt{x}$=1,则x=4.分析 根据对数函数的性质即可求出.
解答 解:log2$\sqrt{x}$=1=log22,
∴$\sqrt{x}$=2,
∴x=4,
故答案为:4.
点评 本题考查了对数方程的解法,属于基础题.

练习册系列答案
相关题目
4.若实数x,y满足不等式组$\left\{\begin{array}{l}{2x+y≤4}\\{x≥0}\\{y≥0}\end{array}\right.$,则$\frac{y+1}{2x+2}$的取值范围是( )
| A. | [$\frac{1}{6}$,$\frac{5}{2}$] | B. | [$\frac{1}{3}$,5] | C. | [$\frac{2}{3}$,10] | D. | [-$\frac{1}{3}$,5] |
2.圆周上有6个点,任取3个点可以做一个三角形,可得到三角形的个数( )
| A. | 6 | B. | 12 | C. | 18 | D. | 20 |
4.已知A、B是半径为R的球O的球面上两点,∠AOB=α,C为球面上的动点,若三棱锥O-ABC的体积最大,则α和最大体积分别为( )
| A. | $\frac{π}{3}$,$\frac{1}{6}$R3 | B. | $\frac{π}{3}$,$\frac{1}{3}$R3 | C. | $\frac{π}{2}$,$\frac{1}{3}$R3 | D. | $\frac{π}{2}$,$\frac{1}{6}$R3 |
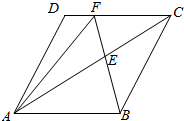 如图,在菱形ABCD中,AB=1,∠BAD=60°,且E为对角线AC上一点.
如图,在菱形ABCD中,AB=1,∠BAD=60°,且E为对角线AC上一点.