题目内容
若三角形三边长之比为 3：5：7，那么这个三角形的最大角是 ．
考点：余弦定理
专题：解三角形
分析：根据题意设出三角形三边，且最大角为α，利用余弦定理表示出cosα，将三边长代入求出cosα的值，即可确定出α的度数．
解答：
解：根据题意设三角形三边长为3x，5x，7x，最大角为α，
由余弦定理得：cosα=
=-
，
则最大角为120°．
故答案为：120．
由余弦定理得：cosα=
| 9x2+25x2-49x2 |
| 30x2 |
| 1 |
| 2 |
则最大角为120°．
故答案为：120．
点评：此题考查了余弦定理，以及特殊角的三角函数值，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
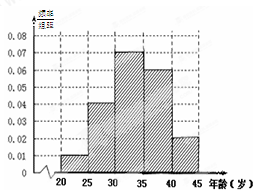上海世博会深圳馆1号作品《大芬丽莎》是由大芬村507名画师集体创作的999幅油画组合而成的世界名画《蒙娜丽莎》，因其诞生于大芬村，因此被命名为《大芬丽莎》．根据如图所示的频率分布直方图，估计这507个画师中年龄不超过30岁的人数约已知f（x）=
，x∈R，求f（
）+f（
）+f（
）+…+f（
）=（ ）
| 4x |
| 4x+2 |
| 1 |
| 1001 |
| 2 |
| 1001 |
| 3 |
| 1001 |
| 1000 |
| 1001 |
| A、499.5 | B、500.5 |
| C、500 | D、499 |
