题目内容
命题“存在x∈R,x3-x3+1>0”的否定是( )
| A、不存在x∈R,x3-x3+1≤0 |
| B、存在x∈R,x3-x3+1≤0 |
| C、对任意的x∈R,x3-x3+1≤0 |
| D、对任意的x∈R,x3-x3+1>0 |
考点:命题的否定
专题:简易逻辑
分析:根据特称命题的否定是全称命题即可得到结论
解答:
解:特称命题的否定是全称命题,
∴命题“存在x∈R,x3-x3+1>0”的否定是:对任意的x∈R,x3-x3+1≤0,
故选:C
∴命题“存在x∈R,x3-x3+1>0”的否定是:对任意的x∈R,x3-x3+1≤0,
故选:C
点评:本题主要考查含有量词的命题的否定,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
等比数列{an}满足,8a2+a5=0,则公比q=( )
| A、2 | B、-2 | C、±2 | D、3 |
设数列{an}的前n项和为Sn,满足2an+1=an+an+2,若 a2+a6+a10是一个定值,则下各数中也为定值( )
| A、S6 |
| B、S11 |
| C、S12 |
| D、S13 |
0<x<3是|x-1|<2成立的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
y=xlnx的导数是( )
| A、x | B、lnx+1 | C、3x | D、1 |
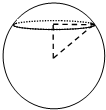 用一平面去截球所得截面的面积为3πcm2,已知球心到该截面的距离为1cm,则该球的体积是
用一平面去截球所得截面的面积为3πcm2,已知球心到该截面的距离为1cm,则该球的体积是