题目内容
|
考点:参数方程化成普通方程,双曲线的简单性质
专题:坐标系和参数方程
分析:利用csc2θ-cot2θ=1可得双曲线方程
-
=1,即可得出渐近线方程.
| x2 |
| 16 |
| y2 |
| 4 |
解答:
解:由
(θ为参数,θ≠kπ,k∈z),利用csc2θ-cot2θ=1可得
-
=1,
∴a=4,b=2,
∴渐近线方程为y=±
x.
故答案为:y=±
x.
|
| x2 |
| 16 |
| y2 |
| 4 |
∴a=4,b=2,
∴渐近线方程为y=±
| 1 |
| 2 |
故答案为:y=±
| 1 |
| 2 |
点评:本题考查了三角函数基本关系式、双曲线的标准方程及其性质,考查了计算能力,属于基础题.

练习册系列答案
相关题目
若a=(
)2,b=log2
,c=2
,则a、b、c的大小关系为.
| 2 |
| 5 |
| 5 |
| 6 |
| 2 |
| 5 |
| A、a<b<c |
| B、b<a<c |
| C、b<c<a |
| D、a<c<b |
在平行四边形ABCD中,AD=2,∠BAD=60°,E为CD的中点,若
•
=1,则AB的长为( )
| AD |
| BE |
A、
| ||
| B、4 | ||
| C、5 | ||
| D、6 |
如图,在矩形ABCD中,AB=3,BC=6,点E为BC的中点,点F在CD边上,若
=2
,则
•
的值为( )

| DF |
| FC |
| AE |
| BF |

| A、-12 | B、12 |
| C、-15 | D、15 |
想要得到函数y=cos2x的图象,只需将函数y=cos(
-2x)( )而得到.
| π |
| 3 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平
|
在18cm长的线段AB上任取一点M,并以线段AM为边作正方形,则点M使得此正方形面积介于25cm2到81cm2之间的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
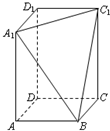 在长方体ABCD-A1B1C1D1中,AD=DC=
在长方体ABCD-A1B1C1D1中,AD=DC=