题目内容
17.已知函数$f(x)=|{x-a}|+\frac{1}{2a}({a≠0})$(1)若不等式f(x)-f(x+m)≤1恒成立,求实数m的最大值;
(2)当a<$\frac{1}{2}$时,函数g(x)=f(x)+|2x-1|有零点,求实数a的取值范围.
分析 (1)若不等式f(x)-f(x+m)≤1恒成立,利用f(x)-f(x+m)=|x-a|-|x+m-a|≤|m|,求实数m的最大值;
(2)当a<$\frac{1}{2}$时,函数g(x)=f(x)+|2x-1|有零点,$g{(x)_{min}}=g({\frac{1}{2}})=\frac{1}{2}-a+\frac{1}{2a}=\frac{{-2{a^2}+a+1}}{2a}≤0$,可得$\left\{\begin{array}{l}0<a<\frac{1}{2}\\-2{a^2}+a+1≤0\end{array}\right.$或$\left\{\begin{array}{l}a<0\\-2{a^2}+a+1≥0\end{array}\right.$,即可求实数a的取值范围.
解答 解:(1)∵$f(x)=|{x-a}|+\frac{1}{2a}$,∴$f({x+m})=|{x+m-a}|+\frac{1}{2a}$,
∴f(x)-f(x+m)=|x-a|-|x+m-a|≤|m|,
∴|m|≤1,∴-1≤m≤1,∴实数m的最大值为1;
(2)当$a<\frac{1}{2}$时,$g(x)=f(x)+|{2x-1}|=|{x-a}|+|{2x-1}|+\frac{1}{2a}$=$\left\{\begin{array}{l}-3x+a+\frac{1}{2a}+1,x<a\\-x-a+\frac{1}{2a}+1,a≤x≤\frac{1}{2}\\ 3x-a+\frac{1}{2a}-1,x>\frac{1}{2}\end{array}\right.$
∴$g{(x)_{min}}=g({\frac{1}{2}})=\frac{1}{2}-a+\frac{1}{2a}=\frac{{-2{a^2}+a+1}}{2a}≤0$,
∴$\left\{\begin{array}{l}0<a<\frac{1}{2}\\-2{a^2}+a+1≤0\end{array}\right.$或$\left\{\begin{array}{l}a<0\\-2{a^2}+a+1≥0\end{array}\right.$,
∴$-\frac{1}{2}≤a<0$,
∴实数a的取值范围是$[{-\frac{1}{2},0})$.
点评 本题考查绝对值不等式的运用,考查分段函数,考查学生分析解决问题的能力,属于中档题.

| A. | $\frac{{8{x^2}}}{9}+\frac{{16{y^2}}}{9}=1$ | B. | $\frac{{9{x^2}}}{8}+\frac{{16{y^2}}}{9}=1$ | C. | $\frac{{8{x^2}}}{9}+\frac{{9{y^2}}}{16}=1$ | D. | $\frac{{9{x^2}}}{8}+\frac{{9{y^2}}}{16}=1$ |
| A. | $-\frac{1}{2}$ | B. | -1 | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |
| A. | (x-1)2+y2=4 | B. | (x-2)2+y2=4 | C. | x2+(y-1)2=4 | D. | (x-1)2+(y-4)2=4 |
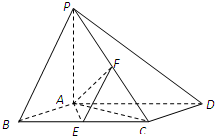 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,