题目内容
已知函数f(x)=log2(x+1),g(x)=log2(4-2x).
(1)求f(x)-g(x)的定义域;
(2)求使f(x)-g(x)>0的x的取值范围.
(1)求f(x)-g(x)的定义域;
(2)求使f(x)-g(x)>0的x的取值范围.
考点:对数函数图象与性质的综合应用
专题:函数的性质及应用
分析:(1)根据对数函数的性质,以及复合函数定义域求法即可得到结论.
(2)利用对数函数的单调性解不等式即可.
(2)利用对数函数的单调性解不等式即可.
解答:
解:(1)∵f(x)=log2(x+1),g(x)=log2(4-2x).
∴f(x)-g(x)=log2(x+1)-log2(4-2x).
要使函数有意义,则
,即
,
则-1<x<2,即函数的定义域为(-1,2).
(2)∵f(x)-g(x)=log2(x+1)-log2(4-2x).-1<x<2,
∴若f(x)-g(x)=log2(x+1)-log2(4-2x)>0,
即log2(x+1)>log2(4-2x),
则x+1>4-2x,即x>1,
∵-1<x<2,∴1<x<2,
故不等式的解集为(1,2).
∴f(x)-g(x)=log2(x+1)-log2(4-2x).
要使函数有意义,则
|
|
则-1<x<2,即函数的定义域为(-1,2).
(2)∵f(x)-g(x)=log2(x+1)-log2(4-2x).-1<x<2,
∴若f(x)-g(x)=log2(x+1)-log2(4-2x)>0,
即log2(x+1)>log2(4-2x),
则x+1>4-2x,即x>1,
∵-1<x<2,∴1<x<2,
故不等式的解集为(1,2).
点评:本题主要考查对数函数的定义域以及与对数函数有关的不等式,利用对数函数的性质是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
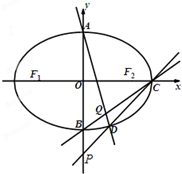 已知F1,F2分别是椭圆E:
已知F1,F2分别是椭圆E: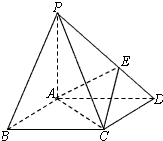 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=1,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=1,PB=PD=