题目内容

3．函数y=x|lnx|的图象大致为（　　）
A．B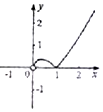．C．D．

分析 通过定义域排除C，D，再取特殊值，x=$\frac{1}{e}$时，y=$\frac{1}{e}$＞0，故排除A，问题得以解决．

解答 解：函数y=x|lnx|的定义域为（0，+∞），故排除C，D，
当x=$\frac{1}{e}$时，y=$\frac{1}{e}$＞0，故排除A，
故选：B

点评 本题考查了函数图象的识别，关键时掌握函数的值域和定义域，属于基础题．

练习册系列答案
相关题目
13．某工艺品厂要设计一个如图Ⅰ所示的工艺品，现有某种型号的长方形材料如图Ⅱ所示，其周长为4m，这种材料沿其对角线折叠后就出现图Ⅰ的情况．如图，ABCD（AB＞AD）为长方形的材料，沿AC折叠后AB'交DC于点P，设△ADP的面积为
S2，折叠后重合部分△ACP的面积为S1．
（Ⅰ）设AB=xm，用x表示图中DP的长度，并写出x的取值范围；
（Ⅱ）求面积S2最大时，应怎样设计材料的长和宽？
（Ⅲ）求面积（S1+2S2）最大时，应怎样设计材料的长和宽？
14．若集合A={-1，0，1，2}，B={y|y=2x+1，x∈A}，则A∪B中元素的个数是（　　）
A．4B．6C．7D．8
11．已知a＞0，a≠1且loga3＞loga2，若函数f（x）=logax在区间[a，2a]上的最大值与最小值之差为1．
（1）求a的值；
（2）解不等式${log_{\frac{1}{3}}}（x-1）＞{log_{\frac{1}{3}}}（a-x）$；
（3）求函数g（x）=|logax-1|的单调区间．
18．设函数f（x），g（x）分别是R上的偶函数和奇函数，则下列结论正确的是（　　）
A．f（x）+g（x）是奇函数B．f（x）-g（x）是偶函数C．f（x）•g（x）是奇函数D．f（x）•g（x）是偶函数
8．已知集合A={1，2，3，4}，B={1，2}，则满足条件B⊆C⊆A的集合C的个数为4．
15．已知函数f（x）=xlnx+$\frac{1}{2}$mx2-（m+1）x+1．
（1）若g（x）=f'（x），讨论g（x）的单调性；
（2）若f（x）在x=1处取得极小值，求实数m的取值范围．
12．已知2sinα+cosα=0，则sin2α-3cos2α-sin2α=（　　）
A．-$\frac{17}{5}$B．-$\frac{17}{4}$C．-$\frac{16}{5}$D．-2
13．下列命题中假命题是（　　）
A．?x∈R，lgx=0B．?x∈R，sinx+cosx=$\sqrt{3}$
C．?x∈R，x2+1≥2xD．?x∈R，2x＞0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网