题目内容
18．实数m分别取什么数值时，复数z=（m2+5m+6）+（m2-2m-15）i：（1）是纯虚数；
（2）对应的点在实轴上方．
分析 （1）由复数z=（m2+5m+6）+（m2-2m-15）i是纯虚数，得实部等于0且虚部不等于0，求解即可得答案；
（2）根据复数z对应点在实轴上方可得m2-2m-15＞0，求解即可得答案．
解答 解：（1）∵复数z=（m2+5m+6）+（m2-2m-15）i是纯虚数，
∴$\left\{\begin{array}{l}{{m}^{2}+5m+6=0}\\{{m}^{2}-2m-15≠0}\end{array}\right.$，解得m=-2．
∴m=-2时，复数z是纯虚数；
（2）由z的对应点在实轴上方，
得m2-2m-15＞0，解得m＜-3或m＞5．
∴m＜-3或m＞5时，复数z对应的点在实轴上方．
点评 本题考查了复数的代数表示法及其几何意义，考查了复数的基本概念，是基础题．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
如图，AB是圆O的直径，点C是圆O上异于A、B的点，直线度PC⊥平面ABC，E、F分别是PA、PC的中点．
10．设x，y，z∈R+，$a=x+\frac{1}{y}，b=y+\frac{1}{z}，c=z+\frac{1}{x}$，则a，b，c三数（ ）
| A． | 都小于2 | B． | 都大于2 | ||
| C． | 至少有一个不大于2 | D． | 至少有一个不小于2 |
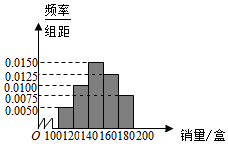某大学在开学季准备销售一种盒饭进行试创业，在一个开学季内，每售出1盒该盒饭获利润10元，未售出的产品，每盒亏损5元．根据历史资料，得到开学季市场需求量的频率分布直方图，如图所示．该同学为这个开学季购进了150盒该产品，以x（单位：盒，100≤x≤200）表示这个开学季内的市场需求量，y（单位：元）表示这个开学季内经销该产品的利润．