题目内容
求函数y=2x2-lnx的单调性.
考点:二次函数的性质
专题:导数的概念及应用
分析:先求出函数的导数,分别令导函数大于0,小于0,解出关于x的范围,从而求出函数的单调性.
解答:
解:∵y=2x2-lnx,(x>0),
∴y′=4x-
=
,
令y′>0,解得:x>
,
令y′<0,解得:0<x<
,
∴函数y=2x2-lnx在(0,
)递减,在(
,+∞)递增.
∴y′=4x-
| 1 |
| x |
| 4x2-1 |
| x |
令y′>0,解得:x>
| 1 |
| 2 |
令y′<0,解得:0<x<
| 1 |
| 2 |
∴函数y=2x2-lnx在(0,
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了函数的单调性,考查导数的应用,是一道基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
函数f(x)=2sin(ωx+ϕ)(ω>0,-
<ϕ<
)的部分图象如图所示,则ω,φ的值分别是( )

| π |
| 2 |
| π |
| 2 |

A、2,-
| ||||
B、2,-
| ||||
C、
| ||||
D、
|
下列判断正确的是( )
| A、命题“a,b都是偶数,则a+b是偶数”的逆否命题是“若a+b不是偶数,则a,b 都不是偶数 |
| B、若“p或q”为假命题,则“¬p且¬q”是假命题 |
| C、已知a,b,c是实数,关于x的不等式ax2+bx+c≤0的解集是空集,必有a>0且∨≤0 |
| D、x2≠y2?x≠y且x≠-y |
已知m,n是满足m+n=1,且使
+
取得最小值的正实数.若曲线y=ax-m+n(a>0且a≠1)恒过定点M,则点M的坐标为( )
| 1 |
| m |
| 4 |
| n |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
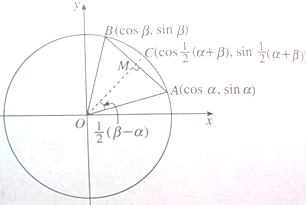 你能利用如图,给出下列两个等式的一个证明吗?
你能利用如图,给出下列两个等式的一个证明吗? 某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/t)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85)[85,90)后得到如图的频率分布直方图.问:
某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/t)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85)[85,90)后得到如图的频率分布直方图.问: