题目内容
19.已知抛物线x2=4y的焦点为F,设A(x1,y1),B(x2,y2)是抛物线上的两个动点,如满足y1+y2+2=$\frac{2\sqrt{3}}{3}$|AB|,则∠AFB的最大值( )| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{6}$ |
分析 由题意画出图形,利用抛物线定义结合已知可得|AF|+|BF|=$\frac{2\sqrt{3}}{3}$|AB|.再由余弦定理,结合基本不等式即可求出∠AFB的最大值.
解答 解:如图,
∵y1+y2+2=$\frac{2\sqrt{3}}{3}$|AB|,又|AF|+|BF|=y1+y2+2,
∴|AF|+|BF|=$\frac{2\sqrt{3}}{3}$|AB|.
在△AFB中,由余弦定理得:cos∠AFB=$\frac{|AF{|}^{2}+|BF{|}^{2}-|AB{|}^{2}}{2|AF|•|BF|}$=$\frac{(|AF|+|BF|)^{2}-2|AF|•|BF|-|AB{|}^{2}}{2|AF|•|BF|}$
=$\frac{\frac{4}{3}|AB{|}^{2}-|AB{|}^{2}}{2|AF|•|BF|}-1$=$\frac{\frac{1}{3}|AB{|}^{2}}{2|AF|•|BF|}-1$.
又|AF|+|BF|=$\frac{2\sqrt{3}}{3}$|AB|≥2$\sqrt{|AF|•|BF|}$,
∴|AF|•|BF|≤$\frac{1}{3}|AB{|}^{2}$.
∴cos∠AFB≥$\frac{\frac{1}{3}|AB{|}^{2}}{2×\frac{1}{3}|AB{|}^{2}}-1=-\frac{1}{2}$,
∴∠AFB的最大值为$\frac{2π}{3}$,
故选:B.
点评 本题考查抛物线的定义,考查余弦定理、基本不等式的运用,属于中档题.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
9.设集合$A=\left\{{({x,y})|{{({x-3})}^2}+{{({y-4})}^2}=\frac{4}{5}}\right\},B=\left\{{({x,y})|{{({x-3})}^2}+{{({y-4})}^2}=\frac{36}{5}}\right\}$,C={(x,y)|2|x-3|+|y-4|=λ},若(A∪B)∩C≠ϕ,则实数λ的取值范围是( )
| A. | $[{\frac{{2\sqrt{5}}}{5},2}]∪[{\frac{{6\sqrt{5}}}{5},6}]$ | B. | $[{\frac{{2\sqrt{5}}}{5},6}]$ | C. | $[{\frac{{2\sqrt{5}}}{5},2}]∪[{4,6}]$ | D. | $\left\{2\right\}∪[{\frac{{6\sqrt{5}}}{5},6}]$ |
11.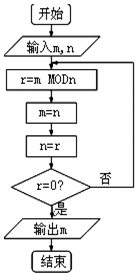 如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“mMODn”表示m除以n的余数),若输入的m,n分别为325,125,则输出的m=( )
如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“mMODn”表示m除以n的余数),若输入的m,n分别为325,125,则输出的m=( )
 如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“mMODn”表示m除以n的余数),若输入的m,n分别为325,125,则输出的m=( )
如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“mMODn”表示m除以n的余数),若输入的m,n分别为325,125,则输出的m=( )| A. | 0 | B. | 5 | C. | 25 | D. | 45 |
9.若$\frac{1+ai}{2+i}=1+2i$,则a=( )
| A. | -5-i | B. | -5+i | C. | 5-i | D. | 5+i |



