题目内容
8.已知单位向量$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$满足$\overrightarrow{a}$=3$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$,且$\overrightarrow{a}$在$\overrightarrow{{e}_{2}}$上的投影为$\frac{1}{2}$,则向量$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$的夹角为$\frac{π}{3}$.分析 设向量$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$的夹角为θ,根据投影的定义即可求出cosθ=$\frac{1}{2}$,问题得以解决
解答 解:设向量$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$的夹角为θ,
∵$\overrightarrow{a}$=3$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$,且$\overrightarrow{a}$在$\overrightarrow{{e}_{2}}$上的投影为$\frac{1}{2}$,
∴$\frac{\overrightarrow{a}•\overrightarrow{{e}_{2}}}{|\overrightarrow{{e}_{2}}|}$=(3$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$)•$\overrightarrow{{e}_{2}}$=3$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$-${\overrightarrow{{e}_{2}}}^{2}$=3×1×1×cosθ-1=$\frac{1}{2}$,
∴cosθ=$\frac{1}{2}$,
∵0≤θ≤π,
∴θ=$\frac{π}{3}$,
故答案为:$\frac{π}{3}$
点评 考查单位向量及投影的定义,数量积的运算及计算公式.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
19.已知抛物线x2=4y的焦点为F,设A(x1,y1),B(x2,y2)是抛物线上的两个动点,如满足y1+y2+2=$\frac{2\sqrt{3}}{3}$|AB|,则∠AFB的最大值( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{6}$ |
13.将函数$y=sin({2x+\frac{π}{6}})$的图象向左平移$\frac{1}{6}$个周期后,所得图象对应的函数g(x)的一个单调增区间为( )
| A. | [0,π] | B. | $[{-\frac{π}{2},0}]$ | C. | $[{0,\frac{π}{2}}]$ | D. | [-π,0] |
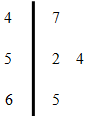 已知某路段最高限速60km/h,电子监控测得连续4辆汽车的速度用用茎叶图表示如图示,若从中任取2辆,则恰好有1辆汽车超速的概率为$\frac{1}{2}$.
已知某路段最高限速60km/h,电子监控测得连续4辆汽车的速度用用茎叶图表示如图示,若从中任取2辆,则恰好有1辆汽车超速的概率为$\frac{1}{2}$.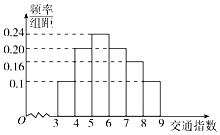 随着社会发展,襄阳市在一天的上下班时段也出现了堵车严重的现象.交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念.记交通指数为T,其范围为[0,10],分别有5个级别:T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3 ),从襄阳市交通指挥中心随机选取了一至四马路之间50个交通路段,依据交通指数数据绘制的直方图如图所示:
随着社会发展,襄阳市在一天的上下班时段也出现了堵车严重的现象.交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念.记交通指数为T,其范围为[0,10],分别有5个级别:T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3 ),从襄阳市交通指挥中心随机选取了一至四马路之间50个交通路段,依据交通指数数据绘制的直方图如图所示: 已知正三棱柱ABC-A1B1C1所有棱长均为2,D、E分别是BC、BB1中点.
已知正三棱柱ABC-A1B1C1所有棱长均为2,D、E分别是BC、BB1中点.