题目内容
9.设集合$A=\left\{{({x,y})|{{({x-3})}^2}+{{({y-4})}^2}=\frac{4}{5}}\right\},B=\left\{{({x,y})|{{({x-3})}^2}+{{({y-4})}^2}=\frac{36}{5}}\right\}$,C={(x,y)|2|x-3|+|y-4|=λ},若(A∪B)∩C≠ϕ,则实数λ的取值范围是( )| A. | $[{\frac{{2\sqrt{5}}}{5},2}]∪[{\frac{{6\sqrt{5}}}{5},6}]$ | B. | $[{\frac{{2\sqrt{5}}}{5},6}]$ | C. | $[{\frac{{2\sqrt{5}}}{5},2}]∪[{4,6}]$ | D. | $\left\{2\right\}∪[{\frac{{6\sqrt{5}}}{5},6}]$ |
分析 集合A、B是表示以(3,4)点为圆心,半径为$\frac{2}{\sqrt{5}}$和$\frac{6}{\sqrt{5}}$的同心圆;
集合C在λ>0时表示以(3,4)为中心,四条边的斜率为±2的菱形;
结合题意画出图形,利用图形知(A∪B)∩C≠∅,
是菱形与A或B圆有交点,从而求得实数λ的取值范围.
解答 解:集合A={(x,y)|(x-3)2+(y-4)2=$\frac{4}{5}$}表示以(3,4)点为圆心,半径为$\frac{2}{\sqrt{5}}$的圆;
集合B={(x,y)|(x-3)2+(y-4)2=$\frac{36}{5}$}表示以(3,4)点为圆心半径为$\frac{6}{\sqrt{5}}$的圆;
集合C={(x,y)|2|x-3|+|y-4|=λ},
∴当x≥3,y≥4时,2|x-3|+|y-4|=λ化为2x+y-10-λ=0;
当x≥3,y<4时,2|x-3|+|y-4|=λ化为2x-y-2-λ=0;
当x<3,y<4时,2|x-3|+|y-4|=λ化为2x+y-10+λ=0;
当x<3,y≥4时,2|x-3|+|y-4|=λ化为2x-y-2+λ=0;
∴在λ>0时,表示以(3,4)为中心,四条边的斜率为±2的菱形,
如下图所示: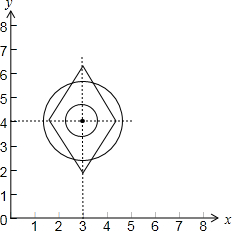
若(A∪B)∩C≠∅,则菱形与A或B圆有交点,
当λ<$\frac{2}{\sqrt{5}}$时,菱形在小圆的内部,与两圆均无交点,不满足答案;
当菱形与小圆相切时,圆心(3,4)到菱形2|x-3|+|y-4|=λ任一边的距离等于大于半径$\frac{2}{\sqrt{5}}$,
当x>3,且y>4时,菱形一边的方程可化为2x+y-(10+λ)=0,
由d=$\frac{|10-(10+λ)|}{\sqrt{{2}^{2}{+1}^{2}}}$=$\frac{2}{\sqrt{5}}$得:λ=2;
当2<λ<$\frac{6}{\sqrt{5}}$时,菱形在大圆的内部,与两圆均无交点,不满足答案;
当菱形与大圆相切时,圆心(3,4)到菱形2|x-3|+|y-4|=λ任一边的距离等于大于半径$\frac{6}{\sqrt{5}}$,
当x>3,且y>4时,菱形一边的方程可化为2x+y-(10+λ)=0,
由d=$\frac{|10-(10+λ)|}{\sqrt{{2}^{2}{+1}^{2}}}$=$\frac{6}{\sqrt{5}}$得:λ=6,
故λ>6时,两圆均在菱形内部,与菱形无交点,不满足答案;
综上实数λ的取值范围是[$\frac{2}{\sqrt{5}}$,2]∪[$\frac{6}{\sqrt{5}}$,6],即[$\frac{2\sqrt{5}}{5}$,2]∪[$\frac{6\sqrt{5}}{5}$,6].
故选:A.
点评 本题考查了集合的基本运算问题,也考查了直线与圆的应用问题,是综合题.

| A. | ${x^2}-\frac{y^2}{3}=1$ | B. | ${x^2}-\frac{y^2}{2}=1$ | C. | ${x^2}-\frac{y^2}{5}=1$ | D. | ${x^2}-\frac{y^2}{6}=1$ |
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{6}$ |
 ,则
,则 ”的否命题是( )
”的否命题是( )
 ,则
,则
 ,则
,则
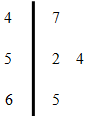 已知某路段最高限速60km/h,电子监控测得连续4辆汽车的速度用用茎叶图表示如图示,若从中任取2辆,则恰好有1辆汽车超速的概率为$\frac{1}{2}$.
已知某路段最高限速60km/h,电子监控测得连续4辆汽车的速度用用茎叶图表示如图示,若从中任取2辆,则恰好有1辆汽车超速的概率为$\frac{1}{2}$.