题目内容
2.在△ABC中,角A,B,C所对应的边长分别为a,b,c,面积为S,若S+a2=(b+c)2,则tanA=( )| A. | $\frac{8}{15}$ | B. | -$\frac{8}{15}$ | C. | $\frac{15}{17}$ | D. | -$\frac{15}{17}$ |
分析 利用三角形面积计算公式、余弦定理可得化为:$\frac{1}{2}$sinA=2cosA+2,与sin2A+cos2A=1,联立解得.
解答 解:由S+a2=(b+c)2,∴$\frac{1}{2}bc$sinA=b2+c2-a2+2bc,化为:$\frac{1}{2}$sinA=2cosA+2,
又sin2A+cos2A=1,A∈(0,π),联立解得sinA=$\frac{8}{17}$,cosA=$-\frac{15}{17}$.
则tanA=$\frac{sinA}{cosA}$=-$\frac{8}{15}$.
故选:B.
点评 本题考查了三角形面积计算公式、余弦定理、同角三角函数基本关系式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
10.满足条件|z-i|+|z+i|=4的复数z在复平面上对应点的轨迹是( )
| A. | 一条直线 | B. | 两条直线 | C. | 圆 | D. | 椭圆 |
17.已知△ABC的边BC上有一点D满足$\overrightarrow{BD}$=3$\overrightarrow{DC}$,则$\overrightarrow{AD}$可表示为( )
| A. | $\overrightarrow{AD}$=-2$\overrightarrow{AB}$+3$\overrightarrow{AC}$ | B. | $\overrightarrow{AD}$=$\frac{3}{4}$$\overrightarrow{AB}$+$\frac{1}{4}$$\overrightarrow{AC}$ | C. | $\overrightarrow{AD}$=$\frac{1}{4}$$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AC}$ | D. | $\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$ |
12.在复平面xOy内,若A(2,-1),B(0,3),则?OACB中,点C对应的复数为( )
| A. | 2+2i | B. | 2-2i | C. | 1+i | D. | 1-i |
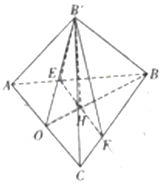 如图,等腰△ABC中,AB=BC=5,AC=6,点E,F分别在AB,BC上,AE=CF=$\frac{5}{4}$,O为AC边上的中点,EF交BO于点H,将△BEF沿EF折到△B′EF的位置,OB′=$\sqrt{10}$.
如图,等腰△ABC中,AB=BC=5,AC=6,点E,F分别在AB,BC上,AE=CF=$\frac{5}{4}$,O为AC边上的中点,EF交BO于点H,将△BEF沿EF折到△B′EF的位置,OB′=$\sqrt{10}$.