题目内容
函数f（x）由下表定义：
若a0=4，an+1=f（an）（n∈N），则a2010的值为（ ）
| x | 1 | 2 | 3 | 4 |
| f（x） | 4 | 1 | 3 | 2 |
| A、1 | B、2 | C、3 | D、4 |
考点：数列的函数特性
专题：计算题,函数思想
分析：利用数列的函数性，再结合函数的周期性求解即可．
解答：
解：∵若a0=4，an+1=f（an）∴a1=f（4）=2，a2=f（2）=1，a3=f（1）=4，a4=f（4）=2，可以看出周期性，周期为3，2010能够被3整除，a2010的值为4
故选：D
故选：D
点评：本题考查了函数的概念，性质在数列求项中的应用．
练习册系列答案
中考解读考点精练系列答案
相关题目
在如图所示的茎叶图中，甲、乙两组数据的中位数分别是．（ ）
| A、42，42 |
| B、45，46 |
| C、35，42 |
| D、47，48 |
函数f（x）=x2+2x-1，x∈[-2，2]的值域为（ ）
A、（
| ||||
| B、（1，2） | ||||
| C、[-2，7] | ||||
| D、[-1，7] |
已知不共线向量
，
满足|
|=2|
|，且关于x的函数f（x）=-2x3+3|
|x2+6
•
x+5在实数集R上是单调递减函数，则向量
，
的夹角的取值范围是（ ）
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| a |
| b |
A、（0，
| ||
B、（0，
| ||
C、[
| ||
D、[
|
“双曲线的方程为
-
=1”是“双曲线的渐近线方程为y=±
x”的（ ）
| x2 |
| 9 |
| y2 |
| 16 |
| 4 |
| 3 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
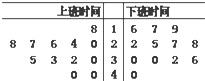
某交警部门对城区上下班交通情况作抽样调查，上下班时间各抽取12辆机动车的行驶速度（单位：km/h）作为样本进行研究，做出样本的茎叶图如图，则上班、下班时间行驶速度的中位数分别是（ ）
| A、28 27.5 |
| B、28 28.5 |
| C、29 27.5 |
| D、29 28.5 |
已知曲线C1：ρ=2和曲线C2：ρcos(θ+
)=
，则C1上到C2的距离等于
的点的个数为（ ）
| π |
| 4 |
| 2 |
| 2 |
| A、0 | B、1 | C、2 | D、3 |
曲线y=
x2-2在x=1处的切线的斜率是（ ）
| 1 |
| 2 |
| A、0 | ||
| B、1 | ||
| C、-1 | ||
D、
|
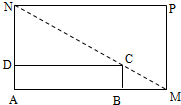如图所示，将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN，要求B在AM上，D在AN上，且对角线MN过C点，已知|AB|=3米，|AD|=2米．