题目内容
19.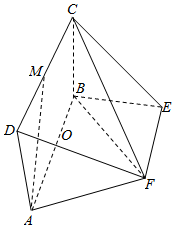 如图所示,平面ABCD⊥平面ABEF,其中四边形ABCD为矩形,四边形ABEF为等腰梯形,AB∥EF,点O为AB的中点,M为CD的中点,AB=2,AF=EF=1
如图所示,平面ABCD⊥平面ABEF,其中四边形ABCD为矩形,四边形ABEF为等腰梯形,AB∥EF,点O为AB的中点,M为CD的中点,AB=2,AF=EF=1(Ⅰ)求证:AF⊥平面CBF;
(Ⅱ)若直线AM与平面CBF所成角的正弦值为$\frac{\sqrt{5}}{10}$,求BC的长.
分析 (Ⅰ)由已知推导出AB⊥BC,从在则BC⊥平面ABEF,进而AF⊥BC,再由余弦定理和勾股定理得到AF⊥BF,由此能证明AF⊥平面CBF.
(Ⅱ)以F为原点,FA为x轴,FB为y轴,过F作平面AFEB的垂线为z轴,建立空间直角坐标系,利用向量法能求出BC的长.
解答 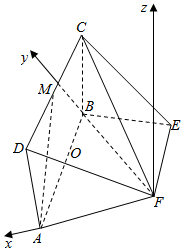 证明:(Ⅰ)∵平面ABCD⊥平面ABEF,其中四边形ABCD为矩形
证明:(Ⅰ)∵平面ABCD⊥平面ABEF,其中四边形ABCD为矩形
∴AB⊥BC,
∵平面ABCD∩平面ABEF=AB,
∴BC⊥平面ABEF,
∵AF?平面ABEF,∴AF⊥BC,
∵四边形ABEF为等腰梯形,AB∥EF,点O为AB的中点,M为CD的中点,AB=2,AF=EF=1,
∴∠BEF=120°,
∴BF=$\sqrt{1+1-2×1×1×cos120°}$=$\sqrt{3}$,
∴AF2+BF2=AF2,∴AF⊥BF,
∵BF∩BC=B,∴AF⊥平面CBF.
解:(Ⅱ)以F为原点,FA为x轴,FB为y轴,过F作平面AFEB的垂线为z轴,建立空间直角坐标系,
设BC=t,由已知得A(1,0,0),D(1,0,t),C(0,$\sqrt{3}$,t),
M($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$,t),B(0,$\sqrt{3}$,0),F(0,0,0),
$\overrightarrow{FB}$=(0,$\sqrt{3}$,0),$\overrightarrow{FC}$=(0,$\sqrt{3}$,t),$\overrightarrow{AM}$=(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$,t),
平面FBC的法向量$\overrightarrow{n}$=(1,0,0),
∵直线AM与平面CBF所成角的正弦值为$\frac{\sqrt{5}}{10}$,
∴|cos<$\overrightarrow{AM},\overrightarrow{n}$>|=$\frac{|\overrightarrow{AM}•\overrightarrow{n}|}{|\overrightarrow{AM}|•|\overrightarrow{n}|}$=$\frac{\frac{1}{2}}{\sqrt{1+{t}^{2}}}$=$\frac{\sqrt{5}}{10}$,
解得t=2或t=-2.(舍)
∴BC的长为2.
点评 本题考查向量垂直的证明,考查线段长的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

| A. | 直线 | B. | 圆 | C. | 椭圆 | D. | 双曲线 |
| A. | 若x0y0∈P且x0y0∉Q | B. | 若x0y0∈Q且x0y0∉P | ||
| C. | 若x0y0∉P且x0y0∉Q | D. | 若x0y0∈P且x0y0∈Q |