题目内容
9.设ax2+bx+1>0的解集是{x|-1<x<2},求a,b.分析 根据不等式ax2+bx+1>0的解集得出对应一元二次方程ax2+bx+1=0的两个实数根,再由根与系数的关系求出a、b的值.
解答 解:不等式ax2+bx+1>0的解集是{x|-1<x<2},
∴一元二次方程ax2+bx+1=0的两个实数根为-1和2,
由根与系数的关系得$\left\{\begin{array}{l}{-1+2=-\frac{b}{a}}\\{-1×2=\frac{1}{a}}\end{array}\right.$,
解得a=-$\frac{1}{2}$,b=$\frac{1}{2}$.
点评 本题考查了一元二次不等式的解集与对应一元二次方程的实数根的应用问题,也考查了根与系数关系的应用问题,是基础题目.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
9. 已知函数f(x)的定义域为[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示.
已知函数f(x)的定义域为[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示.
下列关于函数f(x)的命题:
①函数y=f(x)是周期函数;
②函数f(x)在[0,2]上是减函数;
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为5;
④当1<a<2时,函数y=f(x)-a有4个零点.
其中所有真命题的序号为②③.
 已知函数f(x)的定义域为[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示.
已知函数f(x)的定义域为[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示.| x | -1 | 0 | 4 | 5 |
| f(x) | 1 | 2 | 2 | 1 |
①函数y=f(x)是周期函数;
②函数f(x)在[0,2]上是减函数;
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为5;
④当1<a<2时,函数y=f(x)-a有4个零点.
其中所有真命题的序号为②③.
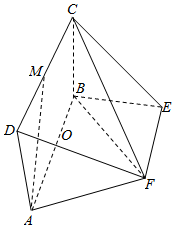 如图所示,平面ABCD⊥平面ABEF,其中四边形ABCD为矩形,四边形ABEF为等腰梯形,AB∥EF,点O为AB的中点,M为CD的中点,AB=2,AF=EF=1
如图所示,平面ABCD⊥平面ABEF,其中四边形ABCD为矩形,四边形ABEF为等腰梯形,AB∥EF,点O为AB的中点,M为CD的中点,AB=2,AF=EF=1