题目内容
9．过三点0（0，0），M（1，1），N（4，2）的圆的方程为x2+y2-8x+6y=0．分析 设所求的圆的方程为x2+y2+Dx+Ey+F=0，把它经过的3个点的坐标代入，解方程组求得D、E、F的值，可得要求的圆的方程．
解答 解：设过三点0（0，0），M（1，1），N（4，2）的圆的方程为x2+y2+Dx+Ey+F=0，
则由$\left\{\begin{array}{l}{F=0}\\{1+1+D+E+F=0}\\{16+4+4D+2E+F=0}\end{array}\right.$求得$\left\{\begin{array}{l}{D=-8}\\{E=6}\\{F=0}\end{array}\right.$，
故要求的圆的方程为x2+y2-8x+6y=0，
故答案为：x2+y2-8x+6y=0．
点评 本题主要考查利用待定系数法求圆的方程，属于基础题．
练习册系列答案
相关题目
19．已知椭圆C的长轴长为10，离心率为$\frac{4}{5}$，则椭圆C的标准方程是（ ）
| A． | $\frac{x^2}{100}+\frac{y^2}{36}$=1 | |
| B． | $\frac{x^2}{100}+\frac{y^2}{36}$=1或 $\frac{x^2}{36}+\frac{y^2}{100}$=1 | |
| C． | $\frac{x^2}{25}+\frac{y^2}{9}$=1 | |
| D． | $\frac{x^2}{25}+\frac{y^2}{9}$=1或 $\frac{x^2}{9}+\frac{y^2}{25}$=1 |
17．设不等式组$\left\{\begin{array}{l}{2x-3y+6≥0}\\{4x-y-8≤0}\\{x+y-2≥0}\end{array}\right.$表示的平面区域为Ω，则当直线y=k（x-1）与区域Ω有公共点时，k的取值范围是（ ）
| A． | [-2，+∞） | B． | （-∞，0] | C． | [-2，0] | D． | （-∞，-2]∪[0，+∞） |
4．已知函数f（x）=sin（ωx-ωπ）（ω＞0）的最小正周期为π，则f（$\frac{π}{12}$）等于（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | -$\frac{\sqrt{3}}{2}$ |
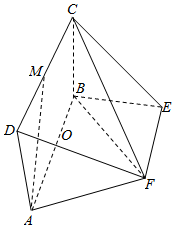如图所示，平面ABCD⊥平面ABEF，其中四边形ABCD为矩形，四边形ABEF为等腰梯形，AB∥EF，点O为AB的中点，M为CD的中点，AB=2，AF=EF=1