题目内容
14.设双曲线方程$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{3}$=1的焦点分别为F1,F2,离心率为2,设A、B分别为双曲线渐近线l1,l2上的动点,且2|AB|=5|F1F2|,则线段AB的中点M的轨迹方程为( )| A. | 直线 | B. | 圆 | C. | 椭圆 | D. | 双曲线 |
分析 设A(x1,y1),B(x2,y2),AB的中点M(x,y),利用2|AB|=5|F1F2|,以及中点坐标公式,建立方程,根据A、B分别为l1、l2上的点,化简可得轨迹方程及对应的曲线.
解答 解:∵e=2,∴c2=4a2,
∵c2=a2+3,∴a=1,c=2,
∴双曲线方程为y2-$\frac{{x}^{2}}{3}$=1,
渐近线方程为y=±$\frac{\sqrt{3}}{3}$x,
设A(x1,y1),B(x2,y2),AB的中点M(x,y),
∵2|AB|=5|F1F2|,
∴|AB|=$\frac{5}{2}$|F1F2|=$\frac{5}{2}$×2c=10,$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$=10,
∵y1=$\frac{\sqrt{3}}{3}$x1,y2=-$\frac{\sqrt{3}}{3}$x2,
2x=x1+x2,2y=y1+y2,
∴y1+y2=$\frac{\sqrt{3}}{3}$(x1-x2),y1-y2=$\frac{\sqrt{3}}{3}$(x1+x2),
即有x1-x2=$\sqrt{3}$(y1+y2),
可得3(2y)2+$\frac{1}{3}$(2x)2=100,
化简可得$\frac{{x}^{2}}{75}$+$\frac{3{y}^{2}}{25}$=1,对应的曲线为椭圆.
故选:C.
点评 本题考查轨迹方程的求解及轨迹的判断,考查双曲线的几何性质,考查学生的计算能力,属于中档题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
4.已知函数f(x)=sin(ωx-ωπ)(ω>0)的最小正周期为π,则f($\frac{π}{12}$)等于( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
5.在(1+$\frac{x}{2}$)(1+$\frac{x}{{2}^{2}}$)…(1+$\frac{x}{{2}^{n}}$)(n∈N+,n≥2)的展开式中,x的系数为$\frac{15}{16}$,则x2的系数为( )
| A. | $\frac{15}{16}$ | B. | $\frac{31}{128}$ | C. | $\frac{35}{128}$ | D. | $\frac{31}{64}$ |
9.设全集U={x∈N*|x≤5},A={1,4},B={4,5},则∁U(A∩B)=( )
| A. | {1,2,3,5} | B. | {1,2,4,5} | C. | {1,3,4,5} | D. | {2,3,4,5} |
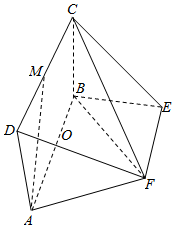 如图所示,平面ABCD⊥平面ABEF,其中四边形ABCD为矩形,四边形ABEF为等腰梯形,AB∥EF,点O为AB的中点,M为CD的中点,AB=2,AF=EF=1
如图所示,平面ABCD⊥平面ABEF,其中四边形ABCD为矩形,四边形ABEF为等腰梯形,AB∥EF,点O为AB的中点,M为CD的中点,AB=2,AF=EF=1