题目内容

4．已知直线l过点（0，-1）且与抛物线y2=4x相交于P，Q两点，弦PQ的中点坐标为（1，b），求此直线方程．

分析 由题意，设直线方程为y=kx-1，代入y2=4x，利用弦PQ的中点坐标为（1，b），求出k，即可求此直线方程．

解答 解：由题意，设直线方程为y=kx-1，代入y2=4x，
整理可得k2x2-（2k+4）x+1=0，
∵弦PQ的中点坐标为（1，b），
∴$\frac{2k+4}{{k}^{2}}$=2，
∴k=2或-1，
∴直线方程为y=2x-1或y=-x-1．

点评 本题考查直线与抛物线的位置关系，考查韦达定理的运用，考查学生的计算能力，属于中档题．

练习册系列答案
相关题目
14．如图，在正方形ABCD中，AD=4，E为DC上一点，且$\overrightarrow{DE}$=3$\overrightarrow{EC}$，则$\overrightarrow{AB}$•$\overrightarrow{AE}$（　　）
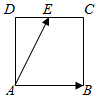
A．20B．16C．15D．12
15．设集合A={a1，a2，…，an}（其中ai∈R，i=1，2，…，n），a0为常数，定义：ω=$\frac{1}{n}$[sin2（a1-a0）+sin2（a2-a0）+…+sin2（an-a0）]为集合A相对a0的“正弦方差”，则集合{$\frac{π}{2}$，π}相对a0的“正弦方差”为$\frac{1}{2}$．
12．已知n=${∫}_{1}^{e}\frac{6}{x}$dx，那么${（{x^2}-\frac{1}{x}）^n}$的展开式中的常数项为15．
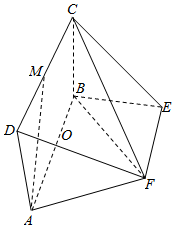19．如图所示，平面ABCD⊥平面ABEF，其中四边形ABCD为矩形，四边形ABEF为等腰梯形，AB∥EF，点O为AB的中点，M为CD的中点，AB=2，AF=EF=1
（Ⅰ）求证：AF⊥平面CBF；
（Ⅱ）若直线AM与平面CBF所成角的正弦值为$\frac{\sqrt{5}}{10}$，求BC的长．
9．已知：$\sqrt{3}$+2sinx=0．
（1）若x∈[-π，π]，求x；
（2）若x∈[0，2π]，求x．
16．若集合M={x|x2-2x-3＜0}，N={x|x＞1}，则M∩N=（　　）
A．（1，3]B．（1，3）C．[1，3）D．[1，3]
13．二项式（$\root{3}{{x}^{2}}$+$\frac{2}{\sqrt{{x}^{3}}}$）12展开式的中间一项为29568x-5．
14．设直线l1：ax+4y-2=0与l2：x+ay-b=0平行，求实数a与b的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网