题目内容
8．设等差数列{an}，前3项和为12，后3项的和为48，共有8项，则它的首项为$\frac{8}{5}$．分析 化简可得a1+a2+a3=3a1+3d=12，a6+a7+a8=3a1+18d=48，从而联立方程解得．
解答 解：由题意知，
a1+a2+a3=3a1+3d=12，
a6+a7+a8=3a1+18d=48，
联立消d可得，
a1=$\frac{8}{5}$，
故答案为：$\frac{8}{5}$．
点评 本题考查了等差数列的性质的判断与应用，属于基础题．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
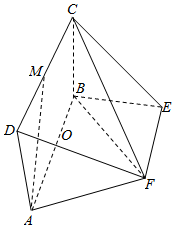如图所示，平面ABCD⊥平面ABEF，其中四边形ABCD为矩形，四边形ABEF为等腰梯形，AB∥EF，点O为AB的中点，M为CD的中点，AB=2，AF=EF=1
16．若集合M={x|x2-2x-3＜0}，N={x|x＞1}，则M∩N=（ ）
| A． | （1，3] | B． | （1，3） | C． | [1，3） | D． | [1，3] |