题目内容
18.已知抛物线C:y2=2px(p>0)的焦点为F,点Q(0,$\sqrt{3}$),射线FQ与C交于点E,与C的准线交于点P,且$\overrightarrow{PE}=2\overrightarrow{EF}$,则点E到y轴的距离是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
分析 由椭圆的定义可知:$\frac{丨EF丨}{丨EP丨}$=$\frac{1}{2}$,即$\frac{丨PK丨}{丨EK丨}$=$\sqrt{3}$,即$\frac{丨OQ丨}{丨OF丨}$=$\frac{\sqrt{3}}{\frac{p}{2}}$,则p=2,求得直线FP的方程,联立即可求得E的横坐标,即可求得点E到y轴的距离.
解答 解:故E作EK⊥准线l,则丨EF丨=丨EK丨,由$\overrightarrow{PE}=2\overrightarrow{EF}$,
则$\frac{丨EF丨}{丨EP丨}$=$\frac{1}{2}$,则$\frac{丨EK丨}{丨EP丨}$=$\frac{1}{2}$,
∴$\frac{丨PK丨}{丨EK丨}$=$\sqrt{3}$,
则tan∠AFO=$\sqrt{3}$,
即$\frac{丨OQ丨}{丨OF丨}$=$\frac{\sqrt{3}}{\frac{p}{2}}$,则p=2,
抛物线方程C:y2=4x,直线FP的方程y=-$\sqrt{3}$(x-1),
$\left\{\begin{array}{l}{y=-\sqrt{3}(x-1)}\\{{y}^{2}=4x}\end{array}\right.$,整理得:3x2-10x+3=0,
解得:x=$\frac{1}{3}$,或x=3,
则E点的横坐标$\frac{1}{3}$,
∴点E到y轴的距离$\frac{1}{3}$,
故选B.
点评 本题考查抛物线的标准方程及抛物线的定义,考查相似三角形的性质,考查数形结合思想,属于中档题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
6.若变量x,y满足约束条件$\left\{\begin{array}{l}{x≥0}\\{x+y≤1}\\{x-y≤1}\end{array}\right.$,则$\frac{y}{x+2}$的最大值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
13.已知复数z=$\frac{2i}{1+i}$,则z•$\overline z$=( )
| A. | 2 | B. | 2i | C. | 4 | D. | 4i |
3.某印刷厂为了研究印刷单册书籍的成本y(单位:元)与印刷册数x(单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
根据以上数据,技术人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲:${\stackrel{∧}{y}}^{(1)}$=$\frac{4}{x}+1.1$,方程乙:$\stackrel{{∧}^{(2)}}{y}$=$\frac{6.4}{x^2}+1.6$.
(1)为了评价两种模型的拟合效果,完成以下任务.
①完成下表(计算结果精确到0.1);
②分别计算模型甲与模型乙的残差平方和Q1及Q2,并通过比较Q1,Q2的大小,判断哪个模型拟合效果更好.
(2)该书上市之后,受到广大读者热烈欢迎,不久便全部售罄,于是印刷厂决定进行二次印刷.根据市场调查,新需求量为8千册(概率0.8)或10千册(概率0.2),若印刷厂以每册5元的价格将书籍出售给订货商,问印刷厂二次印刷8千册还是10千册能获得更多利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本)
| 印刷册数 (千册) | 2 | 3 | 4 | 5 | 8 |
| 单册成本 (元) | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
(1)为了评价两种模型的拟合效果,完成以下任务.
①完成下表(计算结果精确到0.1);
| 印刷册数x(千册) | 2 | 3 | 4 | 5 | 8 | |
| 单册成本y(元) | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
| 模型甲 | 估计值${\stackrel{∧}{{y}_{i}}}^{(1)}$ | 2.4 | 2.1 | 1.6 | ||
| 残差${\stackrel{∧}{{e}_{i}}}^{(1)}$ | 0 | -0.1 | 0.1 | |||
| 模型乙 | 估计值 ${\stackrel{∧}{{y}_{i}}}^{(2)}$ | 2.3 | 2 | 1.9 | ||
| 残差 ${\stackrel{∧}{{e}_{i}}}^{(2)}$ | 0.1 | 0 | 0 | |||
(2)该书上市之后,受到广大读者热烈欢迎,不久便全部售罄,于是印刷厂决定进行二次印刷.根据市场调查,新需求量为8千册(概率0.8)或10千册(概率0.2),若印刷厂以每册5元的价格将书籍出售给订货商,问印刷厂二次印刷8千册还是10千册能获得更多利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本)
1.已知$cosα-sinα=\frac{{\sqrt{2}}}{4}$,则sin2α的值为( )
| A. | $\frac{1}{8}$ | B. | $-\frac{1}{8}$ | C. | $\frac{7}{8}$ | D. | $-\frac{7}{8}$ |
2.椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左焦点为F,点C是椭圆与x轴负半轴的交点,点D是椭圆与y轴正半轴的交点,直线x=m与椭圆相交于A,B两点,若△FAB的周长最大时,CD∥OA(O为坐标原点),则该椭圆的离心率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
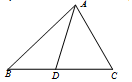 如图,已知△ABC中,D为BC上一点,∠DAC=$\frac{π}{4}$,cos∠BDA=-$\frac{3}{5}$,AC=4$\sqrt{2}$.
如图,已知△ABC中,D为BC上一点,∠DAC=$\frac{π}{4}$,cos∠BDA=-$\frac{3}{5}$,AC=4$\sqrt{2}$.