题目内容
17.在平面直角坐标系xOy中,直线l的参数方程为$\left\{\begin{array}{l}{x=5-t}\\{y=t-1}\end{array}\right.$(t为参数),在以坐标原点为极点,x轴的非负半轴为极轴的极坐标系中,圆C的极坐标方程为ρ=3,则直线l被圆C所截得弦的长度为2.分析 将直线的参数方程化为标准形式,代入圆方程,利用参数的几何意义,即可求弦长.
解答 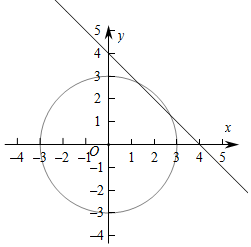 解:曲线C的极坐标方程为ρ=3,化为直角坐标方程为x2+y2=9,
解:曲线C的极坐标方程为ρ=3,化为直角坐标方程为x2+y2=9,
直线l的参数方程为$\left\{\begin{array}{l}{x=5-t}\\{y=t-1}\end{array}\right.$(t为参数),化为标准形式$\left\{\begin{array}{l}{x=5-\frac{\sqrt{2}}{2}t′}\\{y=-1+\frac{\sqrt{2}}{2}t′}\end{array}\right.$,
代入圆方程可得t′2-6$\sqrt{2}$t′+17=0
设方程的根为t′1,t′2,∴t′1+t′2=6$\sqrt{2}$,t′1t′2=17,
∴曲线C被直线l截得的弦长为|t′1-t′2|=$\sqrt{72-68}$=2.
故答案为:2.
点评 本题考查参数方程化为标准方程,极坐标方程化为直角坐标方程,考查参数的几何意义,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
7.设函数g(x)=ex+3x-a(a∈R,e为自然对数底数),若存在x0∈(-∞,1],使g(g(x0))=x0,则实数a的取值范围为( )
| A. | (-∞,$\sqrt{e}$+$\frac{1}{2}$] | B. | (-∞,e+2] | C. | (-∞,e+$\frac{1}{2}$] | D. | (-∞,$\sqrt{e}$+2] |
5.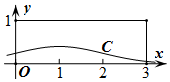 在如图所示的矩形中随机投掷30000个点,则落在曲线C下方(曲线C为正态分布N(1,1)的正态曲线)的点的个数的估计值为( )
在如图所示的矩形中随机投掷30000个点,则落在曲线C下方(曲线C为正态分布N(1,1)的正态曲线)的点的个数的估计值为( )
附:正态变量在区间(μ-σ,μ+σ),(μ-2σ,μ+2σ),(μ-3σ,μ+3σ)内取值的概率分别是0.683,0.954,0.997.
 在如图所示的矩形中随机投掷30000个点,则落在曲线C下方(曲线C为正态分布N(1,1)的正态曲线)的点的个数的估计值为( )
在如图所示的矩形中随机投掷30000个点,则落在曲线C下方(曲线C为正态分布N(1,1)的正态曲线)的点的个数的估计值为( )附:正态变量在区间(μ-σ,μ+σ),(μ-2σ,μ+2σ),(μ-3σ,μ+3σ)内取值的概率分别是0.683,0.954,0.997.
| A. | 4985 | B. | 8185 | C. | 9970 | D. | 24555 |
2.在边长为2的正方形ABCD内部取一点M,则满足∠AMB为锐角的概率是( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{8}$ | C. | $1-\frac{π}{4}$ | D. | $1-\frac{π}{8}$ |
6.若变量x,y满足约束条件$\left\{\begin{array}{l}{x≥0}\\{x+y≤1}\\{x-y≤1}\end{array}\right.$,则$\frac{y}{x+2}$的最大值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
1.已知$cosα-sinα=\frac{{\sqrt{2}}}{4}$,则sin2α的值为( )
| A. | $\frac{1}{8}$ | B. | $-\frac{1}{8}$ | C. | $\frac{7}{8}$ | D. | $-\frac{7}{8}$ |
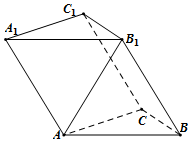 如图,在三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,△ABC和△ABB1都是边长为2的正三角形.
如图,在三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,△ABC和△ABB1都是边长为2的正三角形.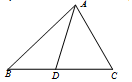 如图,已知△ABC中,D为BC上一点,∠DAC=$\frac{π}{4}$,cos∠BDA=-$\frac{3}{5}$,AC=4$\sqrt{2}$.
如图,已知△ABC中,D为BC上一点,∠DAC=$\frac{π}{4}$,cos∠BDA=-$\frac{3}{5}$,AC=4$\sqrt{2}$.