题目内容
8.数列{an}满足a1=3,${a_n}_{+1}=\left\{\begin{array}{l}2{a_n},\;(0≤{a_n}≤1)\\{a_n}-1,\;\;({a_n}>1).\end{array}\right.$那么a2016=2,数列{an}的前n项和Sn=$\left\{\begin{array}{l}{\frac{3(n+1)}{2},}&{n为奇数}\\{\frac{3n+4}{2},}&{n为偶数}\end{array}\right.$.分析 通过计算数列的前几项,可知数列{an}从第二项起,构成以2为周期的周期数列,进而可知a2016=a2=2,且数列{S2n-1}是首项、公差均为3的等差数列,数列{S2n}是首项为5、公差为3的等差数列,分n为奇数、偶数两种情况讨论即可.
解答 解:依题意,a1=3,
a2=a1-1=2,
a3=a2-1=1,
a4=2a3=2,
…
∴数列{an}从第二项起,构成以2为周期的周期数列,
∵2016=1+2×1007+1,
∴a2016=a2=2,
又∵数列{S2n-1}是首项、公差均为3的等差数列,
数列{S2n}是首项为5、公差为3的等差数列,
∴当n为奇数时,Sn=3+3($\frac{n+1}{2}$-1)=$\frac{3(n+1)}{2}$;
当n为偶数时,Sn=5+3($\frac{n}{2}$-1)=$\frac{3n+4}{2}$;
∴Sn=$\left\{\begin{array}{l}{\frac{3(n+1)}{2},}&{n为奇数}\\{\frac{3n+4}{2},}&{n为偶数}\end{array}\right.$,
故答案为:2,$\left\{\begin{array}{l}{\frac{3(n+1)}{2},}&{n为奇数}\\{\frac{3n+4}{2},}&{n为偶数}\end{array}\right.$.
点评 本题考查数列的通项及前n项和,考查分类讨论的思想,确定周期是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.下列表格中,不是某个随机变量的分布列的是( )
| A. |
| B. |
| ||||||||||||||||||||
| C. |
| D. |
|
13.若f(x)=$\frac{{e}^{x}+{e}^{-x}}{2}$,g(x)=$\frac{{e}^{x}-{e}^{-x}}{2}$则下列等式不正确的是( )
| A. | f(2x)=2g2(x)+1 | B. | f2(x)-g2(x)=1 | C. | f2(x)+g2(x)=f(2x) | D. | f(x+y)=f(x)f(y)-g(x)g(y) |
20.已知抛物线y=4ax2,则其准线方程是( )
| A. | y=-$\frac{1}{16a}$ | B. | x=-a | C. | y=±$\frac{1}{16a}$ | D. | x=±a |
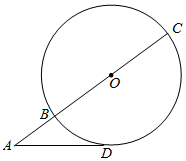 如图,BC为⊙O的直径,且BC=6,延长CB与⊙O在点D处的切线交于点A,若AD=4,则AB=2.
如图,BC为⊙O的直径,且BC=6,延长CB与⊙O在点D处的切线交于点A,若AD=4,则AB=2.