题目内容
14.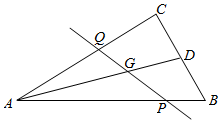 如图,过△ABC的重心G的直线分别交边AB、AC于P、Q两点,且$\overrightarrow{AB}$=x$\overrightarrow{AP}$,$\overrightarrow{AC}$=y$\overrightarrow{AQ}$,则xy的取值范围是[2,$\frac{9}{4}$].
如图,过△ABC的重心G的直线分别交边AB、AC于P、Q两点,且$\overrightarrow{AB}$=x$\overrightarrow{AP}$,$\overrightarrow{AC}$=y$\overrightarrow{AQ}$,则xy的取值范围是[2,$\frac{9}{4}$].
分析 易知存在m,使$\overrightarrow{AG}$=m$\overrightarrow{AQ}$+(1-m)$\overrightarrow{AP}$,且$\overrightarrow{AG}$=$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)=$\frac{1}{3}$(y$\overrightarrow{AQ}$+x$\overrightarrow{AP}$),从而可得x+y=3,且1≤x≤2,从而化为二次函数求范围.
解答 解:∵P,G,Q三点共线,
∴存在m,使$\overrightarrow{AG}$=m$\overrightarrow{AQ}$+(1-m)$\overrightarrow{AP}$,
又∵G是△ABC的重心,
∴$\overrightarrow{AG}$=$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)=$\frac{1}{3}$(y$\overrightarrow{AQ}$+x$\overrightarrow{AP}$),
∴$\frac{1}{3}$(y$\overrightarrow{AQ}$+x$\overrightarrow{AP}$)=m$\overrightarrow{AQ}$+(1-m)$\overrightarrow{AP}$,
∴x+y=3,
又∵$\overrightarrow{AB}$=x$\overrightarrow{AP}$,
∴1≤x≤2,
故xy=x(3-x)=-(x-$\frac{3}{2}$)2+$\frac{9}{4}$,
故2≤-(x-$\frac{3}{2}$)2+$\frac{9}{4}$≤$\frac{9}{4}$,
故答案为:[2,$\frac{9}{4}$].
点评 本题考查了平面向量的线性运算的应用及数形结合的思想应用,同时考查了二次函数的性质应用.

| A. | [-$\sqrt{2}$,0] | B. | [-$\frac{1}{2}$,$\frac{1}{2}$] | C. | [-2,2] | D. | [-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$] |
| A. | 6 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 2 |
| 时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
| 车流量x(万辆) | 100 | 102 | 108 | 114 | 116 |
| PM2.5的浓度y(微克/立方米) | 78 | 80 | 84 | 88 | 90 |
(Ⅱ)若周六同一时间段车流量200万辆,试根据(Ⅰ)求出的线性回归方程,预测此时PM2.5的浓度为多少?
(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$•$\overline{x}$;参考数据:$\sum_{i=1}^{5}$xi=540,$\sum_{i=1}^{5}$yi=420)
| A. | $\frac{5}{3}$ | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |