题目内容
6.已知m>0,n>0,在(1+mx)3+(1+$\sqrt{3}$nx)2的展开式中,当x2项系数为3时,则m+n的最大值为( )| A. | $\frac{5}{3}$ | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
分析 (1+mx)3+(1+$\sqrt{3}$nx)2的展开式中,x2项系数为${∁}_{3}^{2}•{m}^{2}$+3n2,可得m2+n2=1,利用m+n$≤\sqrt{2({m}^{2}+{n}^{2})}$即可得出.
解答 解:(1+mx)3+(1+$\sqrt{3}$nx)2的展开式中,
x2项系数为${∁}_{3}^{2}•{m}^{2}$+3n2=3m2+3n2=3,
化为m2+n2=1,
∵m>0,n>0,
则m+n$≤\sqrt{2({m}^{2}+{n}^{2})}$=$\sqrt{2}$,
当且仅当m=n=$\frac{\sqrt{2}}{2}$时取等号.
∴m+n的最大值为$\sqrt{2}$.
故选:B.
点评 本题考查了二项式定理的应用、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
20.设$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$是两个不共线的向量,已知向量$\overrightarrow{AB}$=2$\overrightarrow{{e}_{1}}$+sinα$\overrightarrow{{e}_{2}}$(-$\frac{π}{2}$<α<$\frac{π}{2}$),$\overrightarrow{CB}$=$\overrightarrow{{e}_{1}}$-$\frac{5}{4}$$\overrightarrow{{e}_{2}}$,$\overrightarrow{CD}$=2$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$,若A、B、D三点共线,则函数f(x)=2cos(x+α)在[0,π)上的值域为( )
| A. | [-1,$\frac{1}{2}$] | B. | [-2,$\sqrt{3}$] | C. | (-2,1] | D. | (-1,$\sqrt{3}$] |
1.某调研机构调取了当地2014年10月~2015年3月每月的雾霾天数与严重交通事故案例数资料进行统计分析,以备下一年如何预防严重交通事故作参考.部分资料如下:
该机构的研究方案是:先从这六组数中剔除2组,用剩下的4组数据求线性回归方程,再用被剔除的2组数据进行检验,若由线性回归方程得到的估计数据与所剔除的检验数据的误差均不超过2,则认为得到的线性回归方程是合情的.
(1)求剔除的2组数据不是相邻2个月数据的概率;
(2)若剔除的是2014年10月与2015年2月这两组数据,请你根据其它4个月的数据,求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(3)①根据(2)所求的回归方程,求2014年10月与2015年2月的严重交通事故案例数;
②判断(2)所求的线性回归方程是否是合情的.
[附:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$.
| 时间 | 14年10月 | 14年11月 | 14年12月 | 15年1月 | 15年2月 | 15年3月 |
| 雾霾天数 | 7 | 11 | 13 | 12 | 10 | 8 |
| 严重交通事故案例数 | 14 | 25 | 29 | 26 | 22 | 16 |
(1)求剔除的2组数据不是相邻2个月数据的概率;
(2)若剔除的是2014年10月与2015年2月这两组数据,请你根据其它4个月的数据,求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(3)①根据(2)所求的回归方程,求2014年10月与2015年2月的严重交通事故案例数;
②判断(2)所求的线性回归方程是否是合情的.
[附:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$.
11.已知集合A={x|y=$\sqrt{x-{x^2}}$),B={y|y-l<0),则A∩B=( )
| A. | (一∞,1) | B. | (一∞,1] | C. | [0,1) | D. | [0,1] |
18.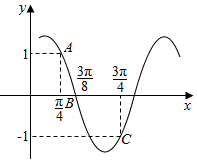 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若tanα=3,则f($α+\frac{π}{8}$)的值为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若tanα=3,则f($α+\frac{π}{8}$)的值为( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若tanα=3,则f($α+\frac{π}{8}$)的值为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若tanα=3,则f($α+\frac{π}{8}$)的值为( )| A. | -$\frac{3}{5}$ | B. | -$\frac{4}{5}$ | C. | -$\frac{3\sqrt{2}}{5}$ | D. | -$\frac{4\sqrt{2}}{5}$ |
16. 对某商店一个月内每天的顾客人数进行统计,得到样本的茎叶图(如图所示).则该样本的中位数、众数、极差分别是( )
对某商店一个月内每天的顾客人数进行统计,得到样本的茎叶图(如图所示).则该样本的中位数、众数、极差分别是( )
 对某商店一个月内每天的顾客人数进行统计,得到样本的茎叶图(如图所示).则该样本的中位数、众数、极差分别是( )
对某商店一个月内每天的顾客人数进行统计,得到样本的茎叶图(如图所示).则该样本的中位数、众数、极差分别是( )| A. | 46 45 56 | B. | 46 45 53 | C. | 47 45 56 | D. | 45 47 53 |
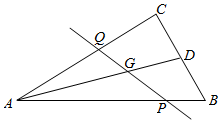 如图,过△ABC的重心G的直线分别交边AB、AC于P、Q两点,且$\overrightarrow{AB}$=x$\overrightarrow{AP}$,$\overrightarrow{AC}$=y$\overrightarrow{AQ}$,则xy的取值范围是[2,$\frac{9}{4}$].
如图,过△ABC的重心G的直线分别交边AB、AC于P、Q两点,且$\overrightarrow{AB}$=x$\overrightarrow{AP}$,$\overrightarrow{AC}$=y$\overrightarrow{AQ}$,则xy的取值范围是[2,$\frac{9}{4}$]. 已知正三角形A1A2A3,A4、A5、A6分别是所在棱的中点,如图,则当1≤i≤6,1≤j≤6,且i≠j时,数量积$\overrightarrow{{A}_{1}{A}_{2}}$•$\overrightarrow{{A}_{i}{A}_{j}}$的不同数量积的个数为9.
已知正三角形A1A2A3,A4、A5、A6分别是所在棱的中点,如图,则当1≤i≤6,1≤j≤6,且i≠j时,数量积$\overrightarrow{{A}_{1}{A}_{2}}$•$\overrightarrow{{A}_{i}{A}_{j}}$的不同数量积的个数为9.