题目内容
8.设点M(x0,x0+$\sqrt{2}$),若在圆O:x2+y2=1上存在点N,使得∠OMN=45°,则x0的取值范围是( )| A. | [-$\sqrt{2}$,0] | B. | [-$\frac{1}{2}$,$\frac{1}{2}$] | C. | [-2,2] | D. | [-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$] |
分析 根据直线和圆的位置关系,作出图象,数形结合可得.
解答 解:∵点M(x0,x0+$\sqrt{2}$)在直线y=x+$\sqrt{2}$上,
又直线y=x+$\sqrt{2}$与圆O:x2+y2=1相切,
∴要使圆O:x2+y2=1上存在点N,使得∠OMN=45°,
则∠OMN的最大值大于或等于45°时,一定存在点N,使得∠OMN=45°,
而当MN与圆相切时∠OMN取得最大值,此时有MN=1,
∴x0的取值范围为[-$\sqrt{2}$,0]
故选:A.
点评 本题考查直线与圆的位置关系,数形结合是解决问题的关键,属中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
18.设p、q是两个命题,若¬(p∨q)是真命题,那么( )
| A. | p是真命题且q是假命题 | B. | p是真命题且q是真命题 | ||
| C. | p是假命题且q是真命题 | D. | p是假命题且q是假命题 |
16.在△ABC中,BC=1,ccosA+acosC=2bcosB,△ABC的面积S=$\sqrt{3}$,则AC等于( )
| A. | $\sqrt{13}$ | B. | 4 | C. | 3 | D. | $\sqrt{15}$ |
3.若方程x3-3ax+2=0(a>0)有三个不同的实根,则实数a的取值范围为( )
| A. | a>0 | B. | 0<a<1 | C. | 1<a<3 | D. | a>1 |
13.若A(xl,y1),B(x2,y2)为平面上两点,则定义A?B=x1y1+x2y2,已知点M($\sqrt{3}$,sinx),N(-1,cosx),设函数f(x)=M?N,将f(x)的图象向左平移φ(φ>0)个单位长度后,所得图象关于y轴对称,则φ的最小值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
20.设$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$是两个不共线的向量,已知向量$\overrightarrow{AB}$=2$\overrightarrow{{e}_{1}}$+sinα$\overrightarrow{{e}_{2}}$(-$\frac{π}{2}$<α<$\frac{π}{2}$),$\overrightarrow{CB}$=$\overrightarrow{{e}_{1}}$-$\frac{5}{4}$$\overrightarrow{{e}_{2}}$,$\overrightarrow{CD}$=2$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$,若A、B、D三点共线,则函数f(x)=2cos(x+α)在[0,π)上的值域为( )
| A. | [-1,$\frac{1}{2}$] | B. | [-2,$\sqrt{3}$] | C. | (-2,1] | D. | (-1,$\sqrt{3}$] |
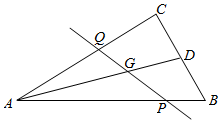 如图,过△ABC的重心G的直线分别交边AB、AC于P、Q两点,且$\overrightarrow{AB}$=x$\overrightarrow{AP}$,$\overrightarrow{AC}$=y$\overrightarrow{AQ}$,则xy的取值范围是[2,$\frac{9}{4}$].
如图,过△ABC的重心G的直线分别交边AB、AC于P、Q两点,且$\overrightarrow{AB}$=x$\overrightarrow{AP}$,$\overrightarrow{AC}$=y$\overrightarrow{AQ}$,则xy的取值范围是[2,$\frac{9}{4}$].