题目内容
函数f（x）=（
） -x2-2x+1的单调区间为 ．
| 1 |
| 2 |
考点：复合函数的单调性
专题：函数的性质及应用
分析：令t=-x2-2x+1，则f（x）=(
)t，则函数t的单调性和函数f（x）=(
)t 的单调性相反．利用二次函数的性质可得函数t=-（x+1）2+2 的单调区间，可得f（x）的单调区间．
| 1 |
| 2 |
| 1 |
| 2 |
解答：
解：令t=-x2-2x+1，则f（x）=g（t）=(
)t，根据复合函数的单调性，函数t=-x2-2x+1的单调性和函数f（x）=(
)t 的单调性相反．
利用二次函数的性质可得函数t=-x2-2x+1=-（x+1）2+2 的增区间为（-∞，-1），减区间为[-1，+∞），
故函数f（x）的减区间为（-∞，-1），增区间为[-1，+∞），
故答案为：减区间为（-∞，-1），增区间为[-1，+∞）．
| 1 |
| 2 |
| 1 |
| 2 |
利用二次函数的性质可得函数t=-x2-2x+1=-（x+1）2+2 的增区间为（-∞，-1），减区间为[-1，+∞），
故函数f（x）的减区间为（-∞，-1），增区间为[-1，+∞），
故答案为：减区间为（-∞，-1），增区间为[-1，+∞）．
点评：本题主要考查复合函数的单调性，二次函数的性质，体现了转化的数学思想，属于中档题．
练习册系列答案
相关题目
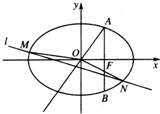如图，已知椭圆C：