题目内容
7. 在三棱柱ABC-A1BlC1中,已知侧棱与底面垂直,∠CAB=90°,且AC=1,AB=2,E为BB1的中点,M为AC上一点,AM=$\frac{2}{3}$AC.
在三棱柱ABC-A1BlC1中,已知侧棱与底面垂直,∠CAB=90°,且AC=1,AB=2,E为BB1的中点,M为AC上一点,AM=$\frac{2}{3}$AC.(I)若三棱锥A1-C1ME的体积为$\frac{{\sqrt{2}}}{6}$,求AA1的长;
(Ⅱ)证明:CB1∥平面A1EM.
分析 (I)由A1A⊥AB,AC⊥AB可知AB⊥平面ACC1A1,故E到平面ACC1A1的距离等于AB,于是VV${\;}_{{A}_{1}-{C}_{1}ME}$=V${\;}_{E-{A}_{1}{C}_{1}M}$,根据体积列出方程解出A1A;
(II)连结AB1交A1E于F,连结MF,由矩形知识可知AF=$\frac{2}{3}A{B}_{1}$,故MF∥CB1,所以CB1∥平面A1EM.
解答 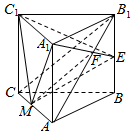 解:(I)∵A1A⊥平面ABC,AB?平面ABC,
解:(I)∵A1A⊥平面ABC,AB?平面ABC,
∴A1A⊥AB,又A1A⊥AC,A1A?平面ACC1A1,AC?平面ACC1A1,A1A∩AC=A,
∴AB⊥平面ACC1A1,
∵BB1∥平面ACC1A1,
∴V${\;}_{{A}_{1}-{C}_{1}ME}$=V${\;}_{E-{A}_{1}{C}_{1}M}$=$\frac{1}{3}{S}_{△{A}_{1}{C}_{1}M}•AB$=$\frac{1}{3}×\frac{1}{2}×{A}_{1}{C}_{1}×{A}_{1}A×AB$=$\frac{1}{3}×\frac{1}{2}×1×{A}_{1}A×2$=$\frac{\sqrt{2}}{6}$.
∴A1A=$\frac{\sqrt{2}}{2}$.
(II)连结AB1交A1E于F,连结MF,
∵E是B1B的中点,
∴AF=$\frac{2}{3}A{B}_{1}$,又AM=$\frac{2}{3}AC$,
∴MF∥CB1,又MF?平面A1ME,CB1?平面A1ME
∴CB1∥平面A1EM.
点评 本题考查了线面平行的判定,棱锥的体积计算,属于基础题.

练习册系列答案
相关题目
17.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一条渐近线的斜率为2,过右焦点F作x轴的垂线交双曲线与A,B两点,△OAB(O为坐标原点)的面积为4$\sqrt{5}$,则F到一条渐近线的距离为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 3 |
15.已知F1、F2分别是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,过点F1的直线与双曲线C的左、右两支分别交于P、Q两点,|F1P|、|F2P|、|F1Q|成等差数列,且∠F1PF2=120°,则双曲线C的离心率是( )
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{7}$ |
17.已知抛物线y2=2x的弦AB的中点坐标为(1,$\frac{\sqrt{2}}{2}$),则|AB|=( )
| A. | 3 | B. | $\sqrt{2}+1$ | C. | $\sqrt{3}+1$ | D. | 4 |
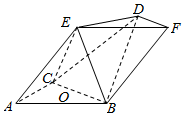 如图,多面体ABCDEF中,四边形ABFE是平行四边形,DF∥BC,BC=BF=2DF=2$\sqrt{2}$,∠BAC=90°,AB=AC,点E在底面ABC的射影为BC的中点O.
如图,多面体ABCDEF中,四边形ABFE是平行四边形,DF∥BC,BC=BF=2DF=2$\sqrt{2}$,∠BAC=90°,AB=AC,点E在底面ABC的射影为BC的中点O.