题目内容
19.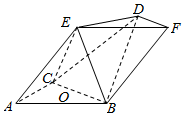 如图,多面体ABCDEF中,四边形ABFE是平行四边形,DF∥BC,BC=BF=2DF=2$\sqrt{2}$,∠BAC=90°,AB=AC,点E在底面ABC的射影为BC的中点O.
如图,多面体ABCDEF中,四边形ABFE是平行四边形,DF∥BC,BC=BF=2DF=2$\sqrt{2}$,∠BAC=90°,AB=AC,点E在底面ABC的射影为BC的中点O.(1)证明:ED⊥平面EBC;
(2)求多面体ABCDEF的体积.
分析 (1)连接AO,DO,EO,利用线面垂直的判定定理证明:AO⊥平面EBC,利用四边形ABFE是平行四边形,证明ED∥AO,即可证明ED⊥平面EBC;
(2)利用V=VE-ABC+VE-BCDF求多面体ABCDEF的体积.
解答 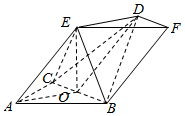 (1)证明:连接AO,DO,EO,则
(1)证明:连接AO,DO,EO,则
∵AB=AC,O为BC的中点,
∴AO⊥BC,
∵点E在底面ABC的射影为BC的中点O,
∴EO⊥平面ABC,
∵AO?平面ABC,∴EO⊥AO,
∵EO∩BC=O,AO⊥BC,EO⊥AO,
∴AO⊥平面EBC.
∵BC=2DF,O为BC的中点,
∴DF=BO
∵DF∥BC,
∴四边形DFBO是平行四边形,
∴BF∥DO,BF=DO
∵四边形ABFE是平行四边形,
∴BF∥AE,BF=AE,
∴BF∥DO,BF=DO,
∴四边形AEDO是平行四边形,
∴ED∥AO,AO⊥平面EBC,
∴ED⊥平面EBC;
(2)解:∵BC=2$\sqrt{2}$,∠BAC=90°,AB=AC,
∴AO=2,
∴DE=2.
∵DO=FB=2$\sqrt{2}$,
∴EO=2.
取DO的中点M,则EM⊥DO.
由(1)可知BO⊥平面EDO,∴BO⊥EM,
∵DO∩BO=O,
∴EM⊥平面DCDF,且EM=$\sqrt{2}$.
∴多面体ABCDEF的体积V=VE-ABC+VE-BCDF=$\frac{1}{3}×\frac{1}{2}×2\sqrt{2}×\sqrt{2}×2$+$\frac{1}{3}×\frac{1}{2}×(\sqrt{2}+2\sqrt{2})×2\sqrt{2}×\sqrt{2}$=$\frac{4}{3}$+2$\sqrt{2}$.
点评 本题考查线面垂直的判定,考查多面体ABCDEF的体积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
9.设双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)与抛物线y2=8x交于两点A,B,且|AB|=8,则该双曲线的焦点到其渐近线的距离为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 4 | D. | $\frac{\sqrt{6}}{3}$ |
10.已知定义在R上的函数f(x)满足f(x-1)=f(1-x),且x≥0时,f(x)=2|x-m|-2,f(-1)=-1,则f(x)<0的解集为( )
| A. | (-∞,-2)∪(2,+∞) | B. | (-2,2) | C. | (0,2) | D. | (-2,0)∪(0,2) |
14.若实数x,y满足条件:$\left\{{\begin{array}{l}{\sqrt{3}x-y≤0}\\{x-\sqrt{3}y+2≥0}\\{y≥0}\end{array}}\right.$,则$\sqrt{3}x+y$的最大值为( )
| A. | 0 | B. | $\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
11.已知双曲线C;$\frac{{y}^{2}}{{b}^{2}+8}$-$\frac{{x}^{2}}{{b}^{2}}$=1(b>0),点P是抛物线y2=12x上的一动点,且P到双曲线C的焦点F1(0,c)的距离与直线x=-3的距离之和的最小值为5,则双曲线C的实轴长为 ( )
| A. | 2$\sqrt{3}$ | B. | 4 | C. | 8 | D. | 4$\sqrt{3}$ |
8.已知双曲线C的两条渐近线为l1,l2,过右焦点F作FB∥l1且交l2于点B,过点B作BA⊥l2且交于l1于点A,若AF⊥x轴,则双曲线C的离心率为( )
| A. | $\sqrt{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | 2$\sqrt{2}$ |
9.设函数f(x)=-2sin(2x+$\frac{π}{4}$),则( )
| A. | y=f(x)在(0,$\frac{π}{8}$)单调递增,其图象关于直线x=$\frac{π}{4}$对称 | |
| B. | y=f(x)在(0,$\frac{π}{8}$)单调递增,其图象关于直线x=$\frac{π}{8}$对称 | |
| C. | y=f(x)在(0,$\frac{π}{8}$)单调递减,其图象关于直线x=$\frac{π}{4}$对称 | |
| D. | y=f(x)在(0,$\frac{π}{8}$)单调递减,其图象关于直线x=$\frac{π}{8}$对称 |
 在三棱柱ABC-A1BlC1中,已知侧棱与底面垂直,∠CAB=90°,且AC=1,AB=2,E为BB1的中点,M为AC上一点,AM=$\frac{2}{3}$AC.
在三棱柱ABC-A1BlC1中,已知侧棱与底面垂直,∠CAB=90°,且AC=1,AB=2,E为BB1的中点,M为AC上一点,AM=$\frac{2}{3}$AC.