题目内容
16.已知底面为正三角形的三棱柱内接于半径为1的球,则三棱柱的体积的最大值为1.分析 设底面边长为a,用a表示出棱柱的高,得出体积关于a的函数,利用导数求出此函数的最大值.
解答 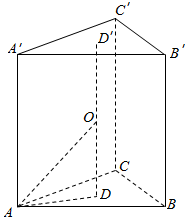 解过球心O作OD⊥平面ABC,则D为正三角形的中心,连结OA,则OA=1.
解过球心O作OD⊥平面ABC,则D为正三角形的中心,连结OA,则OA=1.
设三棱柱的底面边长为a,则AD=$\frac{2}{3}×\frac{\sqrt{3}a}{2}$=$\frac{\sqrt{3}a}{3}$.(0$<a<\sqrt{3}$).
∴OD=$\sqrt{O{A}^{2}-A{D}^{2}}$=$\sqrt{1-\frac{{a}^{2}}{3}}$.
∴棱柱的高DD′=2OD′=2$\sqrt{1-\frac{{a}^{2}}{3}}$.
∴棱柱的体积V=S△ABC•DD′=$\frac{\sqrt{3}}{4}{a}^{2}×2\sqrt{1-\frac{{a}^{2}}{3}}$=$\frac{\sqrt{3{a}^{4}-{a}^{6}}}{2}$.
令f(a)=3a4-a6.
则f′(a)=12a3-6a5=6a3(2-a2),令f′(a)=0得a=$\sqrt{2}$或a=0(舍)或a=-$\sqrt{2}$(舍).
当0<a$<\sqrt{2}$时,f′(a)>0,当$\sqrt{2}$$<a<\sqrt{3}$时,f′(a)<0.
∴当a=$\sqrt{2}$时,f(a)取得最大值f($\sqrt{2}$)=4,
∴当a=$\sqrt{2}$时,V=$\frac{\sqrt{3{a}^{4}-{a}^{6}}}{2}$取得最大值1.
故答案为1.
点评 本题考查了棱柱与外接球的关系,导数与函数最值的关系,属于中档题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
相关题目
6.过双曲线x2-$\frac{y^2}{15}$=1的右支上一点P,分别向圆C1:(x+4)2+y2=4和圆C2:(x-4)2+y2=1作切线,切点分别为M,N,则|PM|2-|PN|2的最小值为( )
| A. | 10 | B. | 13 | C. | 16 | D. | 19 |
11.已知双曲线C;$\frac{{y}^{2}}{{b}^{2}+8}$-$\frac{{x}^{2}}{{b}^{2}}$=1(b>0),点P是抛物线y2=12x上的一动点,且P到双曲线C的焦点F1(0,c)的距离与直线x=-3的距离之和的最小值为5,则双曲线C的实轴长为 ( )
| A. | 2$\sqrt{3}$ | B. | 4 | C. | 8 | D. | 4$\sqrt{3}$ |
8.已知双曲线C的两条渐近线为l1,l2,过右焦点F作FB∥l1且交l2于点B,过点B作BA⊥l2且交于l1于点A,若AF⊥x轴,则双曲线C的离心率为( )
| A. | $\sqrt{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | 2$\sqrt{2}$ |
 在三棱柱ABC-A1BlC1中,已知侧棱与底面垂直,∠CAB=90°,且AC=1,AB=2,E为BB1的中点,M为AC上一点,AM=$\frac{2}{3}$AC.
在三棱柱ABC-A1BlC1中,已知侧棱与底面垂直,∠CAB=90°,且AC=1,AB=2,E为BB1的中点,M为AC上一点,AM=$\frac{2}{3}$AC. 如题(19)图,四边形ABCD为菱形,四边形BDEF为F平行四边形,平面BDEF⊥平面ACE,设AC∩BD=O,AB=AC=2,BF=$\sqrt{3}$.
如题(19)图,四边形ABCD为菱形,四边形BDEF为F平行四边形,平面BDEF⊥平面ACE,设AC∩BD=O,AB=AC=2,BF=$\sqrt{3}$.